题目内容
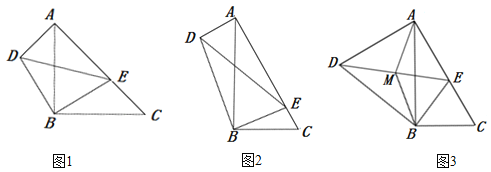
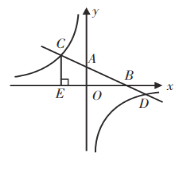
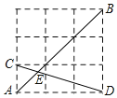
【题目】如图①②,在平面直角坐标系中,边长为2的等边![]() 恰好与坐标系中的
恰好与坐标系中的![]() 重合,现将
重合,现将![]() 绕边
绕边![]() 的中点
的中点![]() 点也是
点也是![]() 的中点),按顺时针方向旋转
的中点),按顺时针方向旋转![]() 到△
到△![]() 的位置.
的位置.
(1)求![]() 点的坐标;
点的坐标;
(2)求经过三点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
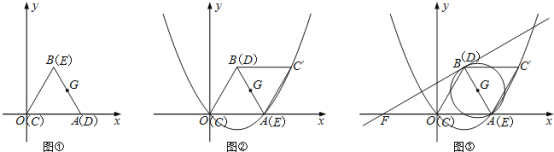
(3)如图③,![]() 是以
是以![]() 为直径的圆,过
为直径的圆,过![]() 点作
点作![]() 的切线与
的切线与![]() 轴相交于点
轴相交于点![]() ,求切线
,求切线![]() 的解析式;
的解析式;
(4)抛物线上是否存在一点![]() ,使得
,使得![]() .若存在,请求出点
.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4) .
.
【解析】
(1)利用中心对称图形的性质和等边三角形的性质,可以求出.
(2)运用待定系数法,代入二次函数解析式,即可求出.
(3)借助切线的性质定理,直角三角形的性质,求出F,B的坐标即可求出解析式.
(4)当M在x轴上方或下方,分两种情况讨论.
解:(1)将等边![]() 绕边
绕边![]() 的中点
的中点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 到△
到△![]() ,
,
则有,四边形![]() 是菱形,所以
是菱形,所以![]() 的横坐标为3,
的横坐标为3,
根据等边![]() 的边长是2,
的边长是2,
利用等边三角形的性质可得![]() ;
;
(2)![]() 抛物线过原点
抛物线过原点![]() ,设抛物线解析式为
,设抛物线解析式为![]() ,
,
把![]() ,
,![]() 代入,得
代入,得 ,
,
解得![]() ,
,![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(3)![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
,![]() 代入,得
代入,得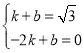 ,
,
解得![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(4)①当![]() 在
在![]() 轴上方时,存在
轴上方时,存在![]() ,
,
![]() ,
,
得![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ;
;
②当![]() 在
在![]() 轴下方时,不存在,设点
轴下方时,不存在,设点![]() ,
,
![]() ,
,
得![]() ,
,![]() 无解,
无解,
综上所述,存在点的坐标为![]() ,
,![]() .
.

 一线名师权威作业本系列答案
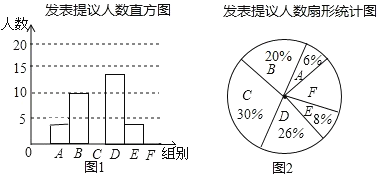
一线名师权威作业本系列答案【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)已知A组发表提议的代表中恰有1位女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.