��Ŀ����
����Ŀ����̽����֪��
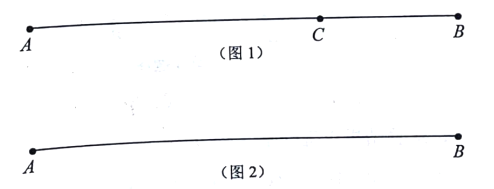
��ͼ1����![]() ���߶�
���߶�![]() �ϣ�ͼ�й���3���߶Σ�
�ϣ�ͼ�й���3���߶Σ�![]() ��
��![]() ��
��![]() ����������һ���߶εij�������һ���߶γ��ȵ���������Ƶ�
����������һ���߶εij�������һ���߶γ��ȵ���������Ƶ�![]() ���߶�
���߶�![]() �ġ������㡱.
�ġ������㡱.
��1����һ���߶ε��е� �����߶εġ������㡱������ǡ����ǡ���
�����߶�![]() ��
��![]() ���߶�
���߶�![]() �ġ������㡱����
�ġ������㡱����![]() ��д�����н����
���������
���������
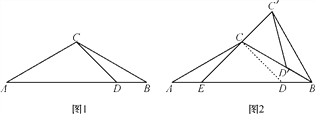
��ͼ2�����߶�![]() ����
����![]() �ӵ�
�ӵ�![]() ��λ�ÿ�ʼ����ÿ��2
��λ�ÿ�ʼ����ÿ��2![]() ���ٶ����
���ٶ����![]() �˶�������
�˶�������![]() �����
�����![]() ʱֹͣ�˶����˶���ʱ��Ϊ
ʱֹͣ�˶����˶���ʱ��Ϊ![]() ��.
��.
��2����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ���߶�
���߶�![]() �ġ������㡱��
�ġ������㡱��
��3��ͬʱ��![]() �ӵ�
�ӵ�![]() ��λ�ÿ�ʼ����ÿ��1
��λ�ÿ�ʼ����ÿ��1![]() ���ٶ����
���ٶ����![]() �˶��������
�˶��������![]() ͬʱֹͣ.��ֱ��д����
ͬʱֹͣ.��ֱ��д����![]() ���߶�
���߶�![]() �ġ������㡱ʱ
�ġ������㡱ʱ![]() ��ֵ.
��ֵ.
���𰸡���1�����ǣ���10��![]() ��
��![]() ����2��5��
����2��5��![]() ��
��![]() ����3��8��
����3��8��![]() ��
��![]()
��������
��1���ٿ�ֱ�Ӹ��ݡ������㡱�Ķ�������жϣ�
�ڿɷ�Ϊ��������������ۣ��ֱ����BC�ij��ȼ��ɣ�
��2���ú�t�Ĵ���ʽ�ֱ��ʾ���߶�AM��BM��AB��Ȼ����ݡ������㡱�����壬�������۵ý����
��3���ú�t�Ĵ���ʽ�ֱ��ʾ���߶�AN��NM��AM��Ȼ����ݡ������㡱�����壬�������ۣ�
�⣺��1������Ϊ�߶ε��е�Ѹ��߶ηֳ���ȵ������֣�
���߶ε���2�����е�һ����߶γ���
��һ���߶ε��е��������߶εġ������㡱
�ʴ�Ϊ����.
�ڡ�![]() ��
��![]() ���߶�
���߶�![]() ��������������
��������������
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�ʴ�Ϊ��10��![]() ��
��![]() ��
��
��2����AM=2BMʱ��20-2t=2��2t����ã�t=![]() ��
��
��AB=2AMʱ��20=2����20-2t������ã�t=5��
��BM=2AMʱ��2t=2����20-2t������ã�t=![]() ��
��
��tΪ![]() ��5��
��5��![]() ʱ����M���߶�AB�ġ������㡱��
ʱ����M���߶�AB�ġ������㡱��
��3����AN=2MNʱ��t=2[t-��20-2t��]����ã�t=8��
��AM=2NMʱ��20-2t=2[t-��20-2t��]����ã�t=![]() ��
��
��MN=2AMʱ��t-��20-2t��=2��20-2t������ã�t=![]() ��
��
��tΪ![]() ��8��
��8��![]() ʱ����M���߶�AN�ġ������㡱��
ʱ����M���߶�AN�ġ������㡱��

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�