题目内容
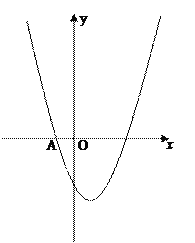
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
① 当点P' 落在该抛物线上时,求m的值;
② 当点P' 落在第二象限内,P'A2取得最小值时,求m的值.
【答案】(1)(1,-4)(2)![]()
【解析】试题分析:
(1)把点A(-1,0)代入抛物线y=x2+bx﹣3解得b的值,即可得到抛物线的解析式;把所得解析式配方化为“顶点式”即可得到抛物线的顶点坐标;
(2)①由点P的坐标(m,t)可得点P′的坐标为(-m,-t),把两点的坐标分别代入(1)中所求抛物线的解析式可得:t=m2﹣2m﹣3,t=﹣m2﹣2m+3,由此可得m2﹣2m﹣3=﹣m2﹣2m+3,解此方程即可求得m的值;
②由P(m,t)在抛物线上可得m2﹣2m=t+3,结合A(﹣1,0),P′(﹣m,﹣t)可得:P′A2=(﹣m+1)2+(﹣t)2=m2﹣2m+1+t2=t2+t+4=(t+![]() )2+
)2+![]() ;由P′(﹣m,﹣t)在第二象限,抛物线顶点坐标为(1,-4)可求得﹣4≤t<0,由此可得当t=﹣
;由P′(﹣m,﹣t)在第二象限,抛物线顶点坐标为(1,-4)可求得﹣4≤t<0,由此可得当t=﹣![]() 时,P′A2有最小值,把t=﹣
时,P′A2有最小值,把t=﹣![]() 代入 t=﹣m2﹣2m+3解方程即可求得此时m的值.
代入 t=﹣m2﹣2m+3解方程即可求得此时m的值.
试题解析:
(1)∵抛物线y=x2+bx﹣3经过点A(﹣1,0),
∴0=1﹣b﹣3,解得b=﹣2,
∴抛物线解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线顶点坐标为(1,﹣4);
(2)①由P(m,t)在抛物线上可得t=m2﹣2m﹣3,
∵点P′与P关于原点对称,
∴P′(﹣m,﹣t),
∵点P′落在抛物线上,
∴﹣t=(﹣m)2﹣2(﹣m)﹣3,即t=﹣m2﹣2m+3,
∴m2﹣2m﹣3=﹣m2﹣2m+3,解得m=![]() 或m=﹣
或m=﹣![]() ;
;
②由题意可知P′(﹣m,﹣t)在第二象限,
∴﹣m<0,﹣t>0,即m>0,t<0,
∵抛物线的顶点坐标为(1,﹣4),
∴﹣4≤t<0,
∵P在抛物线上,
∴t=m2﹣2m﹣3,
∴m2﹣2m=t+3,
∵A(﹣1,0),P′(﹣m,﹣t),
∴P′A2=(﹣m+1)2+(﹣t)2=m2﹣2m+1+t2=t2+t+4=(t+![]() )2+
)2+![]() ;
;
∴当t=﹣![]() 时,P′A2有最小值,
时,P′A2有最小值,
∴﹣![]() =m2﹣2m﹣3,解得m=
=m2﹣2m﹣3,解得m=![]() 或m=
或m=![]() ,
,
∵m>0,
∴m=![]() 不合题意,舍去,
不合题意,舍去,
∴m的值为![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案