题目内容
在△ABC中,∠A=70°,若O为△ABC的外心,则∠BOC=______度;若O为△ABC的内心,则∠BOC=______度.
如图一,点O是三角形的外心.
根据圆周角定理,得
∠BOC=2∠A=140°;
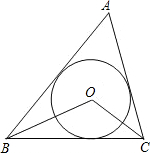
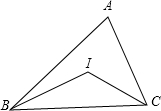
如图二,点O是三角形的内心.
∴BO、CO平分∠ABC、∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A
=125°,
故答案为140°,125°.
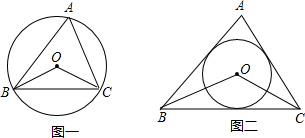
根据圆周角定理,得
∠BOC=2∠A=140°;
如图二,点O是三角形的内心.
∴BO、CO平分∠ABC、∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=125°,
故答案为140°,125°.
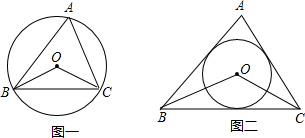

练习册系列答案
相关题目