题目内容
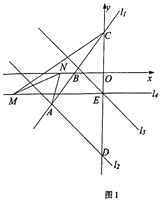
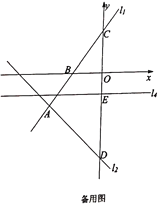
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,已知点
,已知点![]() 的横坐标为-5,直线
的横坐标为-5,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)将直线![]() 向上平移6个单位得到直线
向上平移6个单位得到直线![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,若点
,若点![]() 为垂线
为垂线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
(3)已知点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,是否存在点
,是否存在点![]() 、
、![]() ,使得
,使得![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,若存在,求点
为直角顶点的等腰直角三角形,若存在,求点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(﹣3,
;(3)P(﹣3,![]() ).
).
【解析】
(1)点A在y=-x-8上,点A的横坐标为﹣5,得到A的坐标,将点A代入y![]() x+b,即可求解;
x+b,即可求解;
(2)点D是点C关于直线l4的对称点,作点A关于x轴的对称点A'(﹣5,3),连接AD'交x轴、l4于点N、M,则此时CM+MN+NA最小,最小值为A'D,即可求解;
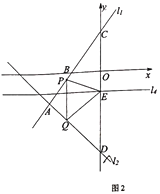
(3)证明△PNQ≌△EKP(AAS),则PN=KE,QN=PK,即可求解.
(1)∵点A在y=-x-8上,点A的横坐标为﹣5,
∴A(﹣5,﹣3).
将点A代入y![]() x+b,
x+b,
∴b=4,
∴直线l1的解析式y![]() x+4;
x+4;
(2)l2:y=﹣x﹣8与y轴的交点D(0,﹣8).
∵将直线l2向上平移6个单位得到直线l3,直线l3与y轴交于点E,
∴E(0,﹣2).
∵过点E作y轴的垂线l4,
点D是点C关于直线l4的对称点,作点A关于x轴的对称点A'(﹣5,3),
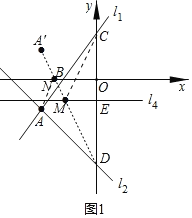
连接AD'交x轴、l4于点N、M,则此时CM+MN+NA最小,最小值为:A'D,
CM+MN+NA=MD+MN+A'N=A'D,
A'D![]() ;∴CM+MN+NA的值最小为
;∴CM+MN+NA的值最小为![]() ;
;
(3)存在,理由:
设点P、Q的坐标分别为:(m,![]() m+4)、(n,﹣n﹣8),
m+4)、(n,﹣n﹣8),
过点Q作x轴的平行线交y轴于点M,过点P作PN⊥QM于点N,PN交l4于点K,

易证△PNQ≌△EKP(AAS),
∴PN=KE,QN=PK,
即:![]() m+4+n+8=﹣m,m﹣n
m+4+n+8=﹣m,m﹣n![]() m+4+2,
m+4+2,
解得:m=﹣3,n=![]() .
.
当m=﹣3时,![]() m+4=
m+4=![]() .
.
故点P(﹣3,![]() ).
).

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案