题目内容
【题目】某水晶厂生产的水晶工艺品非常畅销，某网店专门销售这种工艺品．成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，当x＝40时，y＝300；当x＝55时，y＝150．
（1）求y与x之间的函数关系式；
（2）如果规定每天工艺品的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？
（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该工艺品销售单价的范围．
【答案】（1）
；（2）当销售单价为46元时，每天获取的利润最大，最大利润是3840元；（3）当45≤x≤55时，捐款后每天剩余利润不低于3600元．
【解析】
(1)根据每天销售y(件)与销售单价x(元)之间存在一次函数关系，用待定系数法将
，
，
，
代入
中可求出
和
的值，即可得到
与
之间的函数关系式；(2)设利润为
元，根据每天工艺品的销售量不低于240件求出的范围，再根据总利润=单件利润
销售量得出与之间的函数关系式，根据二次函数的性质求出最值.(3)根据每天捐出150元后每天剩余利润等于3600元列一元二次方程，根据二次函数的图像，求出的范围，即所求销售单价的范围.
(1)设y与x之间的函数关系式：
由题意得：
，解得：
，
∴y与x之间的函数关系式为：
.
(2)设利润为元，
由题意，得
，解得
，
则
，
，
，
∵
，
∴
时，随的增大而增大，
∴
时，
，
答：当销售单价为46元时，每天获取的利润最大，最大利润是3840元.
(3)
，
，
解得：
，
，
结合二次函数图象可得：
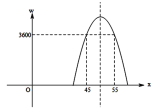
当
时，捐款后每天剩余利润不低于3600元．
【题目】某游泳馆每年夏季推出两种游泳付费方式，方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元．
设小明计划今年夏季游泳次数为x（x为正整数）．
（I）根据题意，填写下表：
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用（元） | 150 | 175 | ______ | … | ______ |
方式二的总费用（元） | 90 | 135 | ______ | … | ______ |
（Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？
（Ⅲ）当x>20时，小明选择哪种付费方式更合算？并说明理由．
