题目内容
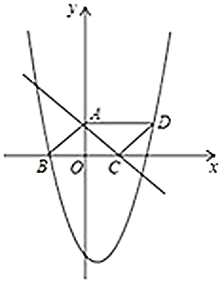
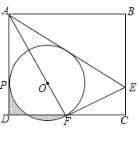
【题目】如图①,在平行四边形ABCD中,对角线AC、BD交于点O,AB=AC,AB⊥AC,过点A作AE⊥BD于点E.
(1)若BC=6![]() ,求AE的长度;
,求AE的长度;
(2)如图②,点F是BD上一点,连接AF,过点A作AG⊥AF,且AG=AF,连接GC交AE于点H,证明:GH=CH.
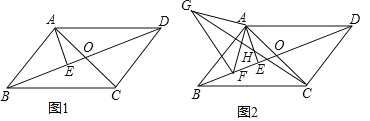
【答案】(1)AE=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意可得:AB=AC=6,可得AO=3,根据勾股定理可求BO的值,根据S△ABO=![]() AB×BO=
AB×BO=![]() BO×AE,可求AE的长度.
BO×AE,可求AE的长度.
(2)延长AE到P,使AP=BF,可证△ABF≌△APC,可得AF=PC.则GA=PC,由AG⊥AF,AE⊥BE可得∠GAH=∠BFA=∠APC,可证△AGH≌△PHC,结论可得.
解:(1)∵AB=AC,AB⊥AC,BC=6![]()
∴AB2+AC2=BC2,
∴2AC2=72
∴AC=AB=6
∵四边形ABCD是平行四边形
∴AO=CO=3
在Rt△AOB中,BO=![]() =3
=3![]()
∵S△ABO=![]() AB×BO=
AB×BO=![]() BO×AE
BO×AE
∴3×6=3![]() ×AE
×AE
∴AE=![]()
(2)如图:延长AE到P,使AP=BF
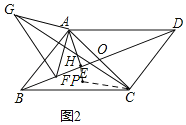
∵∠BAC=90°,AE⊥BE
∴∠BAE+∠ABE=90°,∠BAE+∠CAE=90°
∴∠ABE=∠CAE且AB=AC,BF=AP
∴△ABF≌△APC
∴AF=PC,∠AFB=∠APC
∵AG⊥AF,AG=AF
∴AG=PC
∵∠GAH=∠GAF+∠FAE=90°+∠FAE,∠AFB=∠AEB+∠FAE=90°+∠FAE
∴∠GAH=∠AFB
∴∠AFB=∠GAH=∠APC,且AG=PC,∠GHA=∠CHP
∴△AGH≌△CHP
∴GH=HC

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目