题目内容
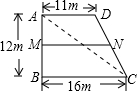
如图，△ABC中，有一点P在AC上移动．若AB=AC=5，BC=6，则AP+BP+CP的最小值为（ ）
| A．8 | B．8.8 | C．9.8 | D．10 |
从B向AC作垂线段BP，交AC于P，
设AP=x，则CP=5-x，
在Rt△ABP中，BP2=AB2-AP2，
在Rt△BCP中，BP2=BC2-CP2，
∴AB2-AP2=BC2-CP2，
∴52-x2=62-（5-x）2
解得x=1.4，
在Rt△ABP中，BP=
=
=4.8，
∴AP+BP+CP=AC+BP=5+4.8=9.8．
故选C．
设AP=x，则CP=5-x，
在Rt△ABP中，BP2=AB2-AP2，
在Rt△BCP中，BP2=BC2-CP2，
∴AB2-AP2=BC2-CP2，
∴52-x2=62-（5-x）2
解得x=1.4，
在Rt△ABP中，BP=
| 52-1.42 |
| 23.04 |
∴AP+BP+CP=AC+BP=5+4.8=9.8．
故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
