题目内容
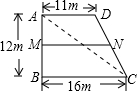
如图所示,在一块形状为直角梯形的草坪中,修建了一条由A→M→N→C的小路(M、N分别是AB、CD中点).极少数同学为了走“捷径”,沿线段AC行走,破坏了草坪,实际上他们仅少走了( )
| A.7米 | B.6米 | C.5米 | D.4米 |

在直角梯形ABCD中,M、N分别是AB、CD的中点,所以MN是梯形的中位线,
∴MN=(AD+BC)÷2,又∵AD=11,BC=16,∴MN=13.5m.
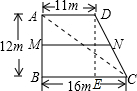
过D点作BC的垂线交BC于点E,则AD=BE=11,DE=AB=12,
又∵BC=BE+CE=16,
∴CE=5,在直角三角形DEC中,DE2+EC2=CD2即122+52=CD2,
∴CD=13,则CN=6.5,
∴AM+MN+NC=6+13.5+6.5=26.
由勾股定理可知AB2+BC2=AC2即122+162=AC2,
∴AC=20,所以他们少走了6m,
故选B.
∴MN=(AD+BC)÷2,又∵AD=11,BC=16,∴MN=13.5m.
过D点作BC的垂线交BC于点E,则AD=BE=11,DE=AB=12,
又∵BC=BE+CE=16,
∴CE=5,在直角三角形DEC中,DE2+EC2=CD2即122+52=CD2,
∴CD=13,则CN=6.5,
∴AM+MN+NC=6+13.5+6.5=26.
由勾股定理可知AB2+BC2=AC2即122+162=AC2,
∴AC=20,所以他们少走了6m,
故选B.


练习册系列答案
相关题目







