Question

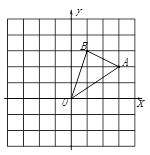
【题目】如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A、B的的坐标分别为A（3，2）、B（1，3）.

⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1，点B1的坐标为 ；

⑵.请画出将△AOB关于原点O成对称的图形△A2OB2，点A2的坐标为 ；

⑶.在x轴上找一点P，使PA+PB的值最小，则P点的坐标为 .

Answer 1

【答案】(1)作图见解析，B1（-2，3）；（2）作图见解析，A2(-3,-2);(3)作图见解析，P(2.2,0).

【解析】试题分析：（1）根据平移规律解答；

（2）根据中心对称图形的概念解答；

（3）根据轴对称-最短路径问题解答．

试题解析：（1）将△AOB向左平移3个单位后得到的图形△A1OB1如图所示，

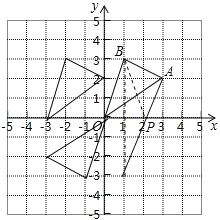
点B1的坐标为（-2，3）；

（2）将△AOB关于原点O成对称的图形△A2OB2如图所示，

点A2的坐标为（-3，-2）；

（3）作点B关于x轴的对称点B′，连接AB′交x轴于点P，则点P即为所求，

点B′的坐标为（1，-3），

设直线AB′的解析式为：y=kx+b，

，

解得，k=，b=-，

则直线AB′的解析式为：y=x-，

x-=0，

解得，x=2.2，

则P点的坐标为（2.2，0），