题目内容
【题目】已知一次函数 y=kx+b（k≠0）的图象经过点(-1，-5)，(2，1)两点．
（1）求 k 和 b 的值；
（2）一次函数 y=kx+b 图象与坐标轴所围成的三角形的面积．
【答案】（1）k=2，b=－3；（2）
【解析】
（1）将两点代入函数，利用待定系数法求得k、b的值；
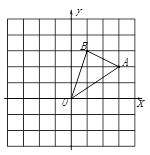
（2）如下图，先求出函数与x轴、y轴的交点，继而求得三角形的底和高，最终求得面积.
将点(-1，-5)，(2，1)代入y=kx+b得：
解读：k=2，b=－3
（2）函数解析式为：y=2x－3
令x=2，y=0－3=－3，∴函数与y轴交于点B(0，－3)
令y=0,0=2x－3，解得：x=
，∴函数与x轴交于点A(，0)，图形如下：
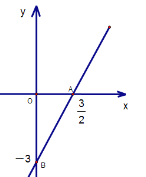
∴AO=，OB=3
∴
练习册系列答案
相关题目
【题目】已知△ABC中，BC边的长为x，BC边上的高为y，△ABC的面积为3．
（1）写出y关于x的函数关系式 ；x的取值范围是 ．
（2）列表，得
x | … | 1 | 2 | 3 | 4 | … |
y | … |
|
|
|
| … |
在给出的坐标系中描点并连线；
（3）如果A（x1，y1），B（x2，y2）是图象上的两个点，且x1＞x2＞0，试判断y1，y2的大小．
