题目内容
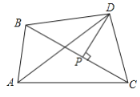
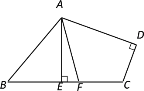
【题目】如图，在四边形ABCD中，∠B＝50°，∠C＝110°，∠D＝90°，AE⊥BC，AF是∠BAD的平分线，与边BC交于点F．求∠EAF的度数．
【答案】15°.
【解析】
先由四边形内角和求出∠BAD的度数，再根据AF是∠BAD的平分线求出∠BAF的值，最后根据直角三角形两锐角互余求出∠BAE即可得到结论.
在四边形ABCD中，∠B＝50°，∠C＝110°，∠D＝90°，
∴∠BAD=360°-∠B-∠C-∠D=360°-50°-110°-90°=110°，
∵AF是∠BAD的平分线，
∴∠BAF=
∠BAD=×110°=55°,
∵AE⊥BC，∠B＝50°，
∴∠BAE=90°-∠B=90°-50°=40°，
∴∠EAF=∠BAF-∠BAE=55°-40°=15°.
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
