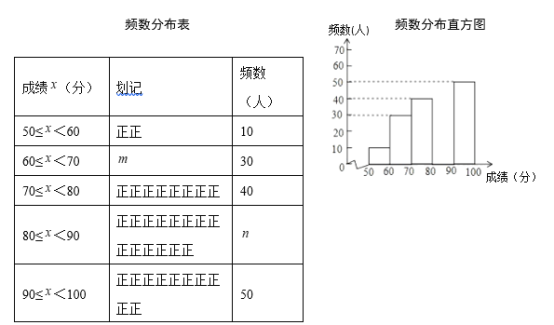
题目内容
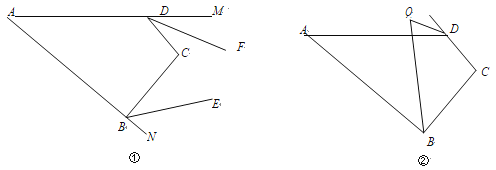
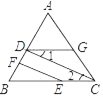
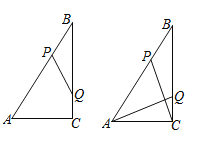
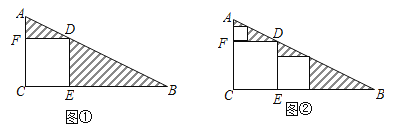
【题目】三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求![]() 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)设CE的长为x,由题意得,AF=1-x,FD=x,由于DF∥BC,根据平行线分线段成比例定理的推论得,ADF∽ABC,根据相似三角形的对应边成比例,得![]() =
=![]() ,即
,即![]() ,解方程得x=
,解方程得x=![]() ,则
,则![]() ,则S1=
,则S1=![]() ×1×2-
×1×2-![]() =
=![]()
(2)第一个图形中,S1=![]() ,即S1是
,即S1是![]() 的
的![]() ;第二个图形中,S2是
;第二个图形中,S2是![]() 和
和![]() 的\和的
的\和的![]() ,即S2=
,即S2=![]() ,…则Sn=
,…则Sn=![]()
【试题解析】
(1)设CE的长为x,由题意得,AF=1-x,FD=x,
∵DF∥BC,∴ADF∽ABC,
∴![]() =
=![]() ,即
,即![]() ,解得x=
,解得x=![]() ,
,
则![]()
则S1=![]() ×1×2-
×1×2-![]() =
=![]()
(2)第一个图形中,S1=![]() ,即S1是
,即S1是![]() 的
的![]() ;第二个图形中,S2是
;第二个图形中,S2是![]() 和
和![]() 的\和的
的\和的![]() ,即S2=
,即S2=![]() ,…,以此类推,则Sn=
,…,以此类推,则Sn=![]()

 阅读快车系列答案
阅读快车系列答案【题目】如图,在矩形ABCD中,AB=6m,BC=12m,点P从点A出发沿AB边向B以1m/s的速度运动,同时点Q从点B出发,沿BC边向点C以2m/s的速度运动,P、Q两点在分别到达B、C两点后就停止运动,设经过ts时,△PBQ的面积为Sm2,则

(1)S与t的函数解析式为:S=_________;
(2)用表格表示:
t/s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
S/m2 |
(3)用图象表示:
(4)在这个问题中,自变量t的取值范围是______;图象的对称轴是_______,顶点坐标是________;当t<______时,S的值随t值的增大而_______;当t>______时,S的值随t值的增大而_______(填“增大”或“减小”);当t=______时,S取得最大值为_______.
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】![]() .
.
【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=![]() .
.
【题型】解答题
【结束】
23
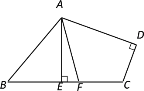
【题目】小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.