��Ŀ����
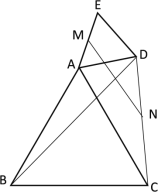
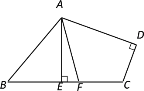
����Ŀ����֪����ͼ1����ƽ��ֱ������ϵ�У���A��B��E�ֱ���x���y���ϵ������. BD�ǡ�ABE��ƽ���ߣ�BD�ķ����ӳ������OAB��ƽ���߽��ڵ�C.
̽���� ��1�����C�Ķ���.
���֣� ��2������A����B�ֱ���x���y������������ƶ�ʱ����C�Ĵ�С�Ƿ����仯�������䣬��ֱ��д�����ۣ��������仯���������C�ı仯��Χ.
Ӧ�ã���3����ͼ2�������ABCDE�У���A����B����E��310����CFƽ�֡�DCB��CF�ķ����ӳ������EDC��ǵ�ƽ�����ཻ�ڵ�P�����P�Ķ�����

���𰸡���1����C=45������2������.��C=![]() ��AOB =45���� (3) 25��.
��AOB =45���� (3) 25��.
��������
��1����ȷ����ABE���OAB�Ĺ�ϵ����ABE=��OAB+90�����ٸ��ݽ�ƽ���ߺ������ε������á�ACB�Ķ�����
��2�����DBC=x����BAC=y���ٸ���BCƽ�֡�DBO��ACƽ�֡�BAO��֪��CBO=��DBC=x����OAC=��BAC=y�����ɡ�DBO����AOB����ǣ���DBC����ABC����ǿɵó�����x��y����C�ķ����飬�����C��ֵ���ɣ�
��3���ӳ�ED��BC�ཻ�ڵ�G�������G�Ķ���������������ǵ����ʿɵý���.
��1���ߡ�ABE=��OAB+��AOB����AOB =90����
���ABE=��OAB+90����
��BD�ǡ�ABE��ƽ���ߣ�ACƽ�֡�OAB��
���ABE=2��ABD����OAB=2��BAC��
��2��ABD=2��BAC+90����
���ABD=��BAC+45����
�֡ߡ�ABD= ��BAC +��C��
���C=45����
��2������.��C=![]() ��AOB =45��.
��AOB =45��.
�������£�
���DBA=x����BAC=y��
��BDƽ�֡�EBA��ACƽ�֡�BAO��
���EBD=��DBA=x����OAC=��BAC=y��
�ߡ�EBA����AOB����ǣ���DBA����ABC����ǣ�
��![]() ��
��
���C=45����
(3) �ӳ�ED��BC�ཻ�ڵ�G.
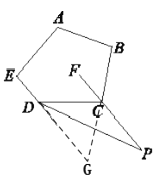
���ı���ABGE�У�
�ߡ�G��360����(��A����B����E)��50����
���P����FCD����CDP��![]() (��DCB����CDG)
(��DCB����CDG)
��![]() ��G��
��G��![]() ��50����25��.
��50����25��.

 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�