题目内容
【题目】已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
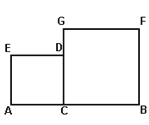
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
【答案】(1)AC=2-x(0≤x≤2)(2)S=2![]() +2(3)4(4)当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处
+2(3)4(4)当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处
【解析】试题分析:(1)、根据AB=2得出AC的长度;(2)、根据总面积等于两个正方形的面积之和得出函数解析式;(3)、根据二次函数的增减性得出面积的最大值和最小值;(4)、根据最值时x的值得出AC的长度,从而得出点C的位置.
试题解析:(1)、当BC=x时,AC=2-x(0≤x≤2);
(2)、S△CDE=![]() ,S△BFG=
,S△BFG=![]() , 因此,S=
, 因此,S=![]() +
+![]() =2
=2![]() -4x+4=2
-4x+4=2![]() +2,
+2,
画出函数S=![]() +2(0≤x≤2)的图象如图:
+2(0≤x≤2)的图象如图:
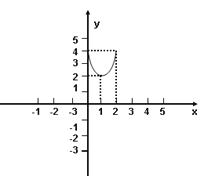
(3)、由图象可知:当x=1时, ![]() ;当x=0或x=2时,
;当x=0或x=2时, ![]() ;
;
(4)、当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目