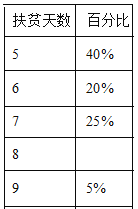
题目内容
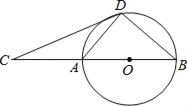
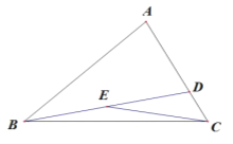
【题目】在![]() 中,点
中,点![]() 在
在![]() 上,
上, ![]() 是
是![]() 中点,
中点,![]() 则
则![]() ___________.
___________.
【答案】![]()
【解析】
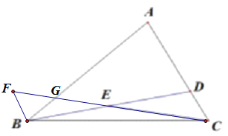
如图,延长CE至F,使得EF=CE,交AB于点G,通过“边角边”证明△BEF≌△DEC,则∠F=∠DCE,BF=DC,根据题意与三角形的外角性质可得∠AGC=∠DCE,进而可得AG=AC,BF=BG=CD,设BF=BG=CD=x,根据题意得到关于x的方程,然后求解方程即可.
如图,延长CE至F,使得EF=CE,交AB于点G,
∵E是BD的中点,
∴BE=DE,
在△BEF与△DEC中,
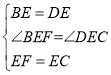 ,
,
∴△BEF≌△DEC(SAS),
∴∠F=∠DCE,BF=DC,
∵![]() ,
,
∴∠DCE=∠ACB﹣∠BCE=![]() ,
,
∵∠AGC=![]() ,
,
∴∠AGC=∠DCE,
∴∠F=∠DCE=∠AGC=∠BGF,AG=AC,
∴BF=BG=CD,
设BF=BG=CD=x,
∵![]() ,
,
∴![]() ,
,
解得x=2,
则CD=2.
故答案为:2.

练习册系列答案
相关题目