题目内容
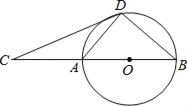
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
【答案】(1)证明见解析;(2)4.
【解析】
(1)连接OD,如图,先证明∠CDA=∠ODB,再根据圆周角定理得∠ADO+∠ODB=90°,则∠ADO+∠CDA=90°,即∠CDO=90°,于是根据切线的判定定理即可得到结论;
(2)由于∠CDA=∠ODB,则tan∠CDA=tan∠ABD=![]() ,根据正切的定义得到tan∠ABD=
,根据正切的定义得到tan∠ABD=![]() ,接着证明△CAD∽△CDB,由相似的性质得
,接着证明△CAD∽△CDB,由相似的性质得![]() ,然后根据比例的性质可计算出CD的长.
,然后根据比例的性质可计算出CD的长.
详(1)证明:连接OD,如图,
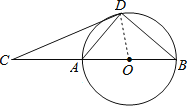
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)∵∠CDA=∠ODB,
∴tan∠CDA=tan∠ABD=![]() ,
,
在Rt△ABD中,tan∠ABD=![]() ,
,
∵∠DAC=∠BDC,∠CDA=∠CBD,
∴△CAD∽△CDB,
∴![]() ,
,
∴CD=![]() ×6=4.
×6=4.

练习册系列答案
相关题目