题目内容
如图,一人行天桥的高是10米,坡面CA的坡角为30°,为了方便行人推车过桥,市政部门决定降低坡度,使新坡面CD的坡角为18°.
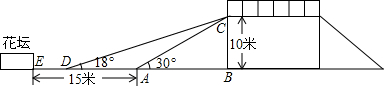
(1)求新坡长CD;(精确到0.01米)
(2)求原坡脚向外延伸后DA的长;(精确到0.01米)
(3)若需留DE为4米的人行道,问离原坡脚A处15米的花坛E是否需要拆除?
(参考数据sin18°=0.309;cos18°=0.951;tan18°=0.325)

(1)求新坡长CD;(精确到0.01米)
(2)求原坡脚向外延伸后DA的长;(精确到0.01米)
(3)若需留DE为4米的人行道,问离原坡脚A处15米的花坛E是否需要拆除?
(参考数据sin18°=0.309;cos18°=0.951;tan18°=0.325)
(1)在Rt△ABC中sin18°=
(1分)
CD=
=
≈32.36(米)(3分)
∴新坡长约为32.36米.(4分)
(2)在Rt△ABC中tan30°=
(1分)
AB=
=
=10
≈17.32(米)(3分)
在Rt△CDB中tan18°=
(4分)
DB=
=
≈30.77(米)(5分)
DA=DB-AB≈30.77-17.32=13.45(米)
∴原坡脚向外延伸约13.45米.(6分)
(3)在Rt△ABC中tan30°=
(1分)
AB=
=10
≈17.32(米)(3分)
在Rt△CDB中tan18°=
(4分)DB=
=
≈30.77(米)(6分)
DA=DB-AB≈30.77-17.32=13.45(米)(7分)4+DA=17.45>15(米)
∴离原坡脚15米的花坛应拆除.(8分)
| CB |
| CD |
CD=
| CB |
| sin18° |
| 10 |
| 0.309 |
∴新坡长约为32.36米.(4分)
(2)在Rt△ABC中tan30°=
| CB |
| AB |
AB=
| CB |
| tan30° |
| 10 | ||||
|
| 3 |
在Rt△CDB中tan18°=
| CB |
| DB |
DB=
| CB |
| tan18° |
| 10 |
| 0.325 |
DA=DB-AB≈30.77-17.32=13.45(米)
∴原坡脚向外延伸约13.45米.(6分)
(3)在Rt△ABC中tan30°=
| CB |
| AB |
AB=
| CB |
| tan30° |
| 3 |
在Rt△CDB中tan18°=
| CB |
| DB |
| CB |
| tan18° |
| 10 |
| 0.325 |
DA=DB-AB≈30.77-17.32=13.45(米)(7分)4+DA=17.45>15(米)
∴离原坡脚15米的花坛应拆除.(8分)

练习册系列答案
相关题目


 一点B,以B为圆心,180m为半径的圆形区域是一个奶牛养殖场.在AD上取一点C,测得AC=200m,点B在点C的北偏西75°方向上.
一点B,以B为圆心,180m为半径的圆形区域是一个奶牛养殖场.在AD上取一点C,测得AC=200m,点B在点C的北偏西75°方向上.