题目内容
已知:PA=
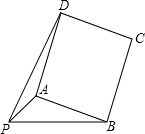
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
| 2 |
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.

(1)①如图,作AE⊥PB于点E,
∵△APE中,∠APE=45°,PA=
,
∴AE=PE=
×
=1,
∵PB=4,∴BE=PB-PE=3,
在Rt△ABE中,∠AEB=90°,
∴AB=
=
.
②解法一:如图,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△P'AB,
可得△PAD≌△P'AB,PD=P'B,PA=P'A.
∴∠PAP'=90°,∠APP'=45°,∠P'PB=90°
∴PP′=
PA=2,
∴PD=P′B=
=
=2
;
解法二:如图,过点P作AB的平行线,与DA的延长线交于F,与DA的
延长线交PB于G.
在Rt△AEG中,
可得AG=
=
=
,EG=
,PG=PE-EG=
.
在Rt△PFG中,
可得PF=PG•cos∠FPG=PG•cos∠ABE=
,FG=
.
在Rt△PDF中,可得,
PD=
=
=2
.
(2)如图所示,

 将△PAD绕点A顺时针旋转90°
将△PAD绕点A顺时针旋转90°
得到△P'AB,PD的最大值即为P'B的最大值,
∵△P'PB中,P'B<PP'+PB,PP′=
PA=2,PB=4,
且P、D两点落在直线AB的两侧,
∴当P'、P、B三点共线时,P'B取得最大值(如图)
此时P'B=PP'+PB=6,即P'B的最大值为6.
此时∠APB=180°-∠APP'=135度.

∵△APE中,∠APE=45°,PA=
| 2 |
∴AE=PE=
| 2 |
| ||
| 2 |
∵PB=4,∴BE=PB-PE=3,
在Rt△ABE中,∠AEB=90°,
∴AB=
| AE2+BE2 |
| 10 |
②解法一:如图,因为四边形ABCD为正方形,可将

△PAD绕点A顺时针旋转90°得到△P'AB,
可得△PAD≌△P'AB,PD=P'B,PA=P'A.
∴∠PAP'=90°,∠APP'=45°,∠P'PB=90°
∴PP′=
| 2 |
∴PD=P′B=
| PP′2+PB2 |
| 22+42 |
| 5 |
解法二:如图,过点P作AB的平行线,与DA的延长线交于F,与DA的
延长线交PB于G.
在Rt△AEG中,

可得AG=
| AE |
| cos∠EAG |
| AE |
| cos∠ABE |
| ||
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
在Rt△PFG中,
可得PF=PG•cos∠FPG=PG•cos∠ABE=
| ||
| 5 |
| ||
| 15 |
在Rt△PDF中,可得,
PD=
| PF2+(AD+AG+FG)2 |
(
|
| 5 |
(2)如图所示,

 将△PAD绕点A顺时针旋转90°
将△PAD绕点A顺时针旋转90°得到△P'AB,PD的最大值即为P'B的最大值,
∵△P'PB中,P'B<PP'+PB,PP′=
| 2 |
且P、D两点落在直线AB的两侧,
∴当P'、P、B三点共线时,P'B取得最大值(如图)
此时P'B=PP'+PB=6,即P'B的最大值为6.
此时∠APB=180°-∠APP'=135度.


练习册系列答案
相关题目
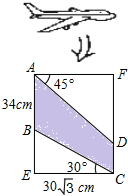

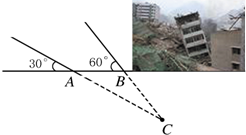
 明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:
明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据: