题目内容
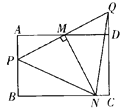
【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问![]() 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;
(2)当△PBN与△NCQ的面积相等时,求AP的值.
【答案】(1)①证明见解析;②![]() 是定值,理由见解析;(2)AP=6
是定值,理由见解析;(2)AP=6
【解析】分析:(1)、①由矩形的性质证明△APM≌△QDM就可以得出PPM=QM,再由MN⊥PQ就可以得出结论;②作ME⊥BC于E,证明△AMP∽△EMN,由相似三角形的性质既可以求出PM与MN的关系,再由勾股定理表示出PN就可以求出结论;(2)、分两种情况,如图2,如图3,作BF⊥PN于F,CG⊥QN于G,作中线BS、CT,通过证明Rt△BFS≌Rt△CGT和△PBN≌△QCN,进一步由全等三角形的性质就可以得出结论.
详解:解(1)①证明:∵四边形ABCD是矩形,∴∠A=∠ADC=∠ADQ=90°,
AB//CD,∴∠APM=∠DQM, ∵M是AD边的中点,∴AM=DM,
在△APM和△DQM中,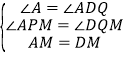 ,∴△APM≌△DQM(AAS),∴PM=QM,
,∴△APM≌△DQM(AAS),∴PM=QM,
∵MN⊥PQ,∴MN是线段PQ的垂直平分线,∴PN=QN,∴∠NPQ=∠PQN;
②解:![]() 是定值
是定值
理由:如图①,过点M作ME⊥BC于点E,∴∠MEN=∠MEB=∠AME=90°,
∴四边形ABEM是矩形,∠MEN=∠MAP,∴AB=EM,
∵MN⊥PQ,∴∠PMN=90°,∴∠PMN=∠AME,
∴∠PMN-∠PME=∠AME-∠PME,∴∠EMN=∠AMP, ∴△AMP∽△EMN,
∴![]() ,∴
,∴![]() ,∵AD=12,M是AD边的中点,∴AM=
,∵AD=12,M是AD边的中点,∴AM=![]() AD=6,
AD=6,
∵AB=8,∴![]() ;
;
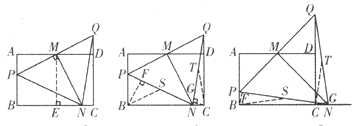
图① 图② 图③
(2)解:分点N在BC之间和点N在BC延长线上两种情况
(ⅰ)当点N在BC之间时,如图②,作BF⊥PN于点F,CG⊥QN于点G,再分别作Rt△PBN和Rt△NCQ的中线BS、CT, ∴∠BFS=∠CGT=90°,BS=![]() PN,CT=
PN,CT=![]() QN,
QN,
∵PN=QN,S△PBN=S△NCQ,∴BF=CG,BS=CT
在Rt△BFS和Rt△CGT中,![]() ,∴Rt△BFS≌Rt△CGT(HL),∴∠BSF=∠CTG,
,∴Rt△BFS≌Rt△CGT(HL),∴∠BSF=∠CTG,
∴∠BNP=![]() ∠BSF=
∠BSF=![]() ∠CTG=∠CQN,
∠CTG=∠CQN,
在△PBN和△NCQ中, ,∴△PBN≌△NCQ(AAS),∴BN=CQ,BP=CN,
,∴△PBN≌△NCQ(AAS),∴BN=CQ,BP=CN,
∵AP=AB-BP=8-CN,又∵CN=BC-BN=12-CQ,∴AP=CQ-4
又∵CQ=CD+DQ,DQ=AP,∴AP=4+AP(舍去),∴此种情况不成立;
(ⅱ)当点N在BC延长线上时,如图③,作BF⊥PN于点F,CG⊥QN于点G,再分别作Rt△PBN和Rt△NCQ的中线BS、CT, 同理可得,△PBN≌△NCQ,∴PB=NC,BN=CQ,
∵AP=DQ, ∵AP+8=DQ+CD=CQ=BC+CN=12+BP,
∴AP-BP=4 ①, ∵AP+BP=AB=8②, ①+②得:2AP=12,∴AP=6.

【题目】某厂按用户的月需求量x (件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本为y (万元),y与x的关系式为![]() (a,b为常数).经市场调研发现,月需求量x与月份n (n为整数,1≤n≤12)的关系式为x=n2-13n+72,且得到了下表中的数据.
(a,b为常数).经市场调研发现,月需求量x与月份n (n为整数,1≤n≤12)的关系式为x=n2-13n+72,且得到了下表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
(1)请直接写出a,b的值;
(2)设第n个月的利润为w(万元),请求出W与n的函数关系式,并求出这一年的12个月中,哪个月份的利润为84万元?
(3)在这一年的前8个月中,哪个月的利润最大?最大利润是多少?
【题目】某影院共有15排座位,第一排有12个座位数,从第2排开始,每一排都比前一排增加2个座位.
(1)请你在下表的空格里填写一个适当的式子.
第1排的座位数 | 第2排的座位数 | 第3排的座位数 | … | 第 |
12 | 14 | 16 | … |
(2)影院最后两排共有多少个座位?