题目内容
如图所示，四边形ABCD是以O为圆心，AB为直径的半圆的内接四边形，对角线AC、BD相交于
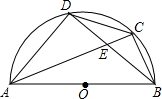
点E．
（1）求证：△DEC∽△AEB；
（2）当∠AED=60°时，求△DEC与△AEB的面积比．
点E．
（1）求证：△DEC∽△AEB；
（2）当∠AED=60°时，求△DEC与△AEB的面积比．
（1）证明：∵∠CDE=∠EAB，∠DCE=∠EBA，
∴△DEC∽△AEB．
（2）∵AB是直径，
∴∠ADB=90度．
∵∠AED=60°，
∴∠DAE=30度．
∴AE=2DE．
∴S△DEC：S△AEB=DE2：AE2=1：4．
∴△DEC∽△AEB．
（2）∵AB是直径，
∴∠ADB=90度．
∵∠AED=60°，
∴∠DAE=30度．
∴AE=2DE．
∴S△DEC：S△AEB=DE2：AE2=1：4．
练习册系列答案
相关题目
21、如图所示，四边形ABCD是平行四边形，E，F分别在AD，CB的延长线上，且DE=BF，连接FE分别交AB，CD于点H，G．
12、如图所示，四边形ABCD为⊙O的内接四边形，E为AB延长线的上一点，∠CBE=40°，则∠AOC等于（ ）
如图所示，四边形ABCD中，E、F分别为AD、BC的中点．
