题目内容
如图所示，四边形ABCD是正方形，E、F是AB、BC的中点，连接EC交DB、DF于G、H，则EG：GH：HC=
分析：过点G作GP∥BC交DF于P，设GH=2a，则由平行线的性质可得
=
=
=
=
，即HC=3a，进而即可得出结论．
| GH |
| HC |
| PG |
| CF |
| PG |
| BF |
| DG |
| BD |
| 2 |
| 3 |
解答：解：过点G作GP∥BC交DF于P，
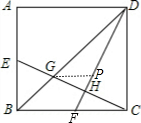
则
=
=
=
=
，
设GH=2a，则HC=3a，可得EG=
，
∴EG：GH：HC=5：4：6．
故答案为：5：4：6．
则
| GH |
| HC |
| PG |
| CF |
| PG |
| BF |
| DG |
| BD |
| 2 |
| 3 |
设GH=2a，则HC=3a，可得EG=
| 5a |
| 2 |
∴EG：GH：HC=5：4：6．
故答案为：5：4：6．
点评：本题主要考查了平行线分线段成比例的性质以及正方形的一些性质问题，要求学生能够利用其性质求解一些简单的计算问题．
练习册系列答案
名校课堂系列答案
相关题目
21、如图所示，四边形ABCD是平行四边形，E，F分别在AD，CB的延长线上，且DE=BF，连接FE分别交AB，CD于点H，G．
12、如图所示，四边形ABCD为⊙O的内接四边形，E为AB延长线的上一点，∠CBE=40°，则∠AOC等于（ ）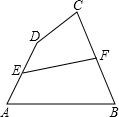
如图所示，四边形ABCD中，E、F分别为AD、BC的中点．