题目内容
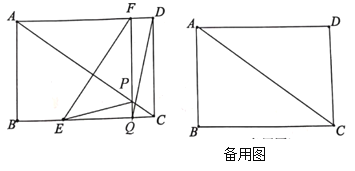
【题目】如图,正方形ABCD的边长为2cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.点H在圆弧上运动上,点H所运动的圆弧的长为______.
【答案】![]()
【解析】
先根据全等三角形的性质证明∠AHB=90°,即点H是以AB为直径的圆上一点,再根据弧长公式求解即可得到答案.
∵ABCD是正方形
∴AD=CD=AB,∠BAD=∠ADC=90°,∠ADB=∠BDC=45°
∵AD=CD,∠ADB=∠BDC,DG=DG
∴△ADG≌△DGC
∴∠DAM=∠DCF且AD=CD,∠ADC=∠ADC
∴△ADM≌△CDF
∴FD=DM且AE=DF
∴AE=DM且AB=AD,∠ADM=∠BAD=90°
∴△ABE≌△ADM(SAS),
∴∠DAM=∠ABE,
∵∠DAM+∠BAM=90°,
∴∠BAM+∠ABE=90°,
即∠AHB=90°,
∴点H是以AB为直径的圆上一点,
以AB的中心O为圆心,以OA为半径画弧,与BD交于I,如图:
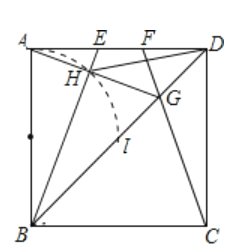
当E点运动到D的位置以及F点运动到A的位置时,是H运动的轨迹的一个端点,
此时,I刚好与H重合(恰好是正方形的中心),
∴此时的圆心角恰好是90°,
根据弧长公式得到H运动的弧长为:![]() ,
,
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目