Question

【题目】如图，直线y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y＝﹣x2+bx+c经过点A，B．

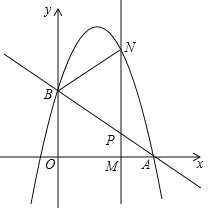
（1）求点B的坐标和抛物线的解析式；

（2）M（m，0）为线段OA上一个动点，过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N．

①试用含m的代数式表示线段PN的长；

②求线段PN的最大值．

Answer 1

【答案】（1）B（0，2），y＝﹣x2+x+2；（2）①PN＝﹣（0≤m≤3）；②m＝时，线段PN有最大值为3．

【解析】

（1）把A点坐标代入直线解析式可求得c，则可求得B点坐标，由A、B的坐标，利用待定系数法可求得抛物线解析式；

（2）①M（m，0），则P（m，），N（m，﹣），即可求出PN的长；

②根据二次函数的性质可得线段PN的最大值．

解：（1）∵y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，

∴0＝﹣2+c，解得c＝2，

∴B（0，2），

∵抛物线y＝﹣x2+bx+c经过点A，B，

∴，解得，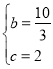

∴抛物线解析式为y＝﹣x2+x+2；

（2）①M（m，0），则P（m，），N（m，﹣），

∴PN＝＝﹣（0≤m≤3）；

②∵PN＝﹣＝，

∴m＝时，线段PN有最大值为3．