Question

【题目】在平面直角坐标系中，已知点A（2，0），点B（0，2），点O（0，0）．△AOB绕着O顺时针旋转，得△A′OB′，点A、B旋转后的对应点为A′、B′，记旋转角为α．

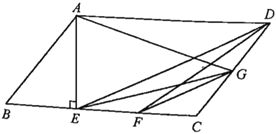
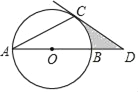
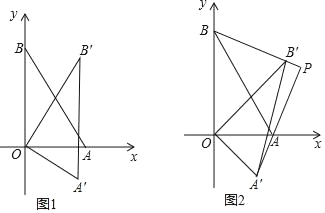
（I）如图1，若α=30°，求点B′的坐标；

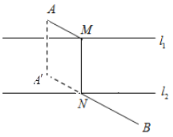
（Ⅱ）如图2，若0°＜α＜90°，设直线AA′和直线BB′交于点P，求证：AA′⊥BB′；

（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．

Answer 1

【答案】（1）B'的坐标为（，3）；（2）见解析 ；（3）﹣2．

【解析】

（1）设A'B'与x轴交于点H，由OA=2，OB=2，∠AOB=90°推出∠ABO=∠B'=30°，

由∠BOB'=α=30°推出BO∥A'B'，由OB'=OB=2推出OH=OB'=，B'H=3即可得出；

（2）证明∠BPA'=90即可；

（3）作AB的中点M（1，），连接MP，由∠APB=90°，推出点P的轨迹为以点M为圆心，以MP=AB=2为半径的圆，除去点（2，），所以当PM⊥x轴时，点P纵坐标的最小值为﹣2．

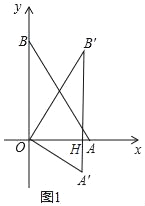
（Ⅰ）如图1，设A'B'与x轴交于点H，

∵OA=2，OB=2，∠AOB=90°，

∴∠ABO=∠B'=30°，

∵∠BOB'=α=30°，

∴BO∥A'B'，

∵OB'=OB=2，

∴OH=OB'=，B'H=3，

∴点B'的坐标为（，3）；

（Ⅱ）证明：∵∠BOB'=∠AOA'=α，OB=OB'，OA=OA'，

∴∠OBB'=∠OA'A=（180°﹣α），

∵∠BOA'=90°+α，四边形OBPA'的内角和为360°，

∴∠BPA'=360°﹣（180°﹣α）﹣（90°+α）=90°，

即AA'⊥BB'；

（Ⅲ）点P纵坐标的最小值为．

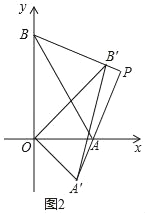
如图，作AB的中点M（1，），连接MP，

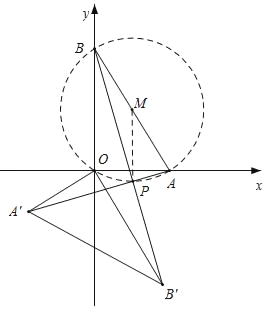
∵∠APB=90°，

∴点P的轨迹为以点M为圆心，以MP=AB=2为半径的圆，除去点（2，）．

∴当PM⊥x轴时，点P纵坐标的最小值为﹣2．