Question

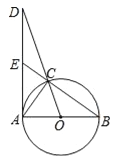
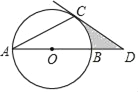
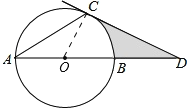
【题目】如图，AB是圆O的直径，AC是圆O的弦，过点C的切线交AB的延长线于点D，若∠A=∠D，CD=2．

（1）求∠A的度数．

（2）求图中阴影部分的面积．

Answer 1

【答案】(1) ∠A=30°;(2)

【解析】

（1）连接OC，由过点C的切线交AB的延长线于点D，推出OC⊥CD，推出∠OCD=90°，即∠D+∠COD=90°，由OA=OC，推出∠A=∠ACO，由∠A=∠D，推出∠A=∠ACO=∠D

再由∠A+∠ACD+∠D=180°﹣90°=90°即可得出.

（2）先求∠COD度数及OC长度，即可求出图中阴影部分的面积．

解：（1）连结OC

∵CD为⊙O的切线

∴OC⊥CD

∴∠OCD=90°

又∵OA=OC

∴∠A=∠ACO

又∵∠A=∠D

∴∠A=∠ACO=∠D

而∠A+∠ACD+∠D=180°﹣90°=90°

∴∠A=30°

（2）由（1）知：∠D=∠A=30°

∴∠COD=60°

又∵CD=2

∴OC=2

∴S阴影=．