题目内容
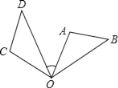
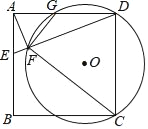
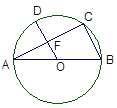
【题目】如图,A,B,C三点在⊙O上,且AB是⊙O的直径,半径OD⊥AC,垂足为F,若∠A=30,OF=3,则OA=_____,AC=_____,BC=_____.
【答案】6, 6![]() , 6
, 6
【解析】
先根据直角三角形的性质求出OA的长,故可得出AB的长,再根据圆周角定理求出∠ACB的度数,由直角三角形的性质求出AB的长,在Rt△ABC中由勾股定理即可求出AC的长.
解:∵OD⊥AC,∠A=30°,OF=3,
∴∠AFO=90°,
∴OA=2OF=2×3=6,
∴AB=2OA=2×6=12,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC=![]() AB=
AB=![]() ×12=6,
×12=6,
在Rt△ABC中,∵AB=12,BC=6,
∴AC=![]() =6
=6![]() .
.
故答案为:6,6![]() ,6.
,6.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目