题目内容
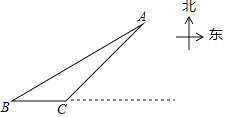
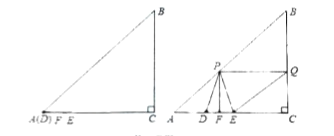
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,长为4cm的线段DE在边AC上,且点D与点A重合,点F是DE的中点,线段DE从点A出发,沿AC方向向点C匀速运动,直到点E与点C重合,速度1cm/s。过点F作PF⊥AC,交AB于点P,过点P作PQ//AC,交BC于点Q,连接PD,PE,QE,设线段DE的运动时间为t(s).(0≤t≤6)
(1)请分别用含有t的代数式表示线段PF、BQ
(2)当t为何值时,四边形PFCQ为正方形?
(3)设四边形PDEQ的面积为y(cm)请求出y与t之间的函数关系式,并求出当t为何值时,四边形PDEQ的面积最大,最大是多少?
(4)是否存在某一时刻t,使得EP平分∠AEQ?若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)PF=t+2,BQ=8-t;(2)t=3s;(3)t=5,y=24.5;(4)存在.![]() 时,EP平分∠AEQ
时,EP平分∠AEQ
【解析】
(1)根据∠C=90°,AC=BC=10cm,可得∠A=![]() ,再根据PF⊥AC可得AF=PF,根据题意可得AF=t+2,CF=8-t,即可得出答案。
,再根据PF⊥AC可得AF=PF,根据题意可得AF=t+2,CF=8-t,即可得出答案。
(2)当PF=PQ时,四边形PFCQ为正方形,列出方程即可。
(3)用矩形DFCQ的面积加上三角形PDF的面积,再减去三角形QEC的面积得到四边形PDEQ的面积,列出y与t的函数关系式即可。
(4)先假设得EP平分∠AEQ,则∠AEP=∠QEP, 再根据 PQ//AC,得出∠AEP=∠QPE, ∠QEP=∠QPE,得出QE=QP,列出方程,方程有解就存在,没解就不存在。
(1)∵∠C=90°,AC=BC=10cm,∴∠A=∠B=![]() , ∵PF⊥AC,∴∠AFP=90°, ∴AF=PF,同理可证,BQ=PQ,∵点F是DE的中点,DE=4,∴DF=EF=2, ∴AF=t+2,∴PF=t+2,则CF=AC-AF=8-t,∵PF⊥AC,∠C=90°,PQ//AC,则四边形PFCQ是矩形,∴PQ=CF, BQ=CF = 8-t;
, ∵PF⊥AC,∴∠AFP=90°, ∴AF=PF,同理可证,BQ=PQ,∵点F是DE的中点,DE=4,∴DF=EF=2, ∴AF=t+2,∴PF=t+2,则CF=AC-AF=8-t,∵PF⊥AC,∠C=90°,PQ//AC,则四边形PFCQ是矩形,∴PQ=CF, BQ=CF = 8-t;
(2)∵四边形PFCQ为正方形,∴PF= CF,∴t+2=8-t,∴t=3,∴t=3时四边形PFCQ为正方形。
(3)y=![]() =(t+2)(8-t)+
=(t+2)(8-t)+![]() 2(t+2)-
2(t+2)-![]() (10-t-4)(t+2)
(10-t-4)(t+2)
∴y=-![]() +5t+12,∵a=-
+5t+12,∵a=-![]() 0,∴当t=5时,
0,∴当t=5时,![]() =24.5
=24.5
∴当t=5时,四边形PDEQ的面积最大,最大面积为24.5
(4)∵EP平分∠AEQ,∴∠AEP=∠QEP, ∵PQ//AC,∴∠AEP=∠QPE, ∴∠QEP=∠QPE, ∴QE=QP=8-t, ∴在Rt![]() ECQ中,
ECQ中,![]() ∴
∴![]()
解得:t=![]() ,t=
,t=![]() (舍去)
(舍去)
∴存在![]() 时,EP平分∠AEQ
时,EP平分∠AEQ

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.
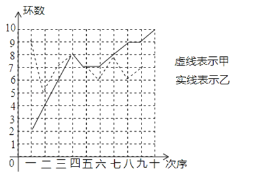
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环以上(包括9环)次数 | |
甲 | 7 |
|
|
|
乙 |
| 5.4 |
|
|
(2)请你就下列两个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环(包括9环)以上次数相结合看(分析谁的潜能更大).