题目内容
如图,点M是反比例函数y= 在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=
在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=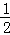 A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=
A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=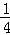 A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=
A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=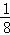 A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .
A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .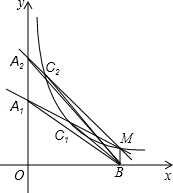
 在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=
在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=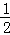 A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=
A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=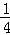 A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=
A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=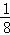 A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .
A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .
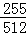
试题分析:根据点M是反比例函数y=
 在第一象限内图象上的点,即可得出
在第一象限内图象上的点,即可得出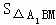 =
= OB×MB=
OB×MB= ,再利用C1到BM的距离为A1到BM的距离的一半,得出S1=
,再利用C1到BM的距离为A1到BM的距离的一半,得出S1=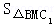 =
=
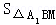 =
= ,同理即可得出S2=
,同理即可得出S2=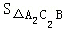 =
=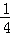
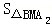 =
=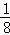 ,S3=
,S3=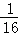 ,S4=
,S4=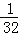 …,进而求出S1+S2+S3+…+S8的值即可.
…,进而求出S1+S2+S3+…+S8的值即可.过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,
∵点M是反比例函数y=
 在第一象限内图象上的点,
在第一象限内图象上的点,∴OB×BM=1,
∴
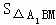 =
= OB×MB=
OB×MB= ,
,∵A1C1=
 A1M,即C1为A1M中点,
A1M,即C1为A1M中点,∴C1到BM的距离C1F为A1到BM的距离A1E的一半,
∴S1=
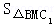 =
=
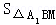 =
= ,
,∴
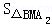 =
= BM•A2到BM距离=
BM•A2到BM距离= ×BM×BO=
×BM×BO= ,
,∵A2C2=
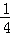 A2M,
A2M,∴C2到BM的距离为A2到BM的距离的
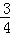 ,
,∴S2=
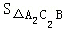 =
=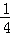
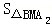 =
=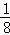 ,
,同理可得:S3=
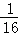 ,S4=
,S4=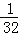 …
…∴
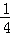 +
+ +…+
+…+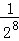 +
+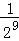 ,=
,= +
+ +…+
+…+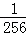 +
+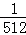 =
=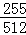 .
.点评:根据同底三角形对应高的关系得出面积关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (度)与镜片焦距
(度)与镜片焦距 (米)成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数
(米)成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数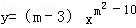 是反比例函数.
是反比例函数.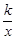 图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是 _______ ______
图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是 _______ ______
 的图象在第二、第四象限,那么m可能取的一个值为
的图象在第二、第四象限,那么m可能取的一个值为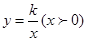 的图象上,矩形ABCD的边BC在
的图象上,矩形ABCD的边BC在 轴上,E是对角线BD的中点,函数
轴上,E是对角线BD的中点,函数
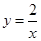 (
(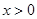 )图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )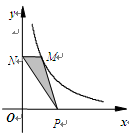
 ,k<0的图象上有两点(-1,y1),(-
,k<0的图象上有两点(-1,y1),(- ,y2),
,y2),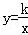 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)