Question

【题目】如图，已知一次函数y=kx+b的图象交反比例函数 图象于点A，B，交x轴于点C．

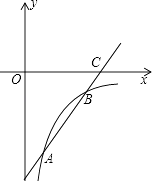
（1）求m的取值范围；
（2）若点A的坐标是（1，﹣4），且 ，求m的值和一次函数的解析式；
（3）在（2）的情况下，请直接写出不等式 的解集．

Answer 1

【答案】
（1）解：因为反比例函数 的图象在第四象限，

所以4﹣2m＜0，解得m＞2．

（2）解：因为点A（1，﹣4）在函数 图象上，

所以﹣4=4﹣2m，解得m=4．

过点A、B分别作AM⊥OC于点M，BN⊥OC于点N，

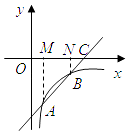
所以∠BNC=∠AMC=90°，

又因为∠BCN=∠ACM，

所以△BCN∽△ACM，所以 ．

因为 ，所以 ，即 ．

因为AM=4，所以BN=1．

所以点B的纵坐标是﹣1．

因为点B在反比例函数 的图象上，所以当y=﹣1时，x=4．

所以点B的坐标是（4，﹣1）．

因为一次函数y=kx+b的图象过点A（1，﹣4）、B（4，﹣1），

所解得 ，

解得：k=1，b=﹣5

所以一次函数的解析式是y=x﹣5；

（3）解：由函数图象可知不等式 的解集为：0＜x＜1 或 x＞4．
【解析】（1）根据双曲线位于第四象限可得到比例系数k＜0，即4-2m＜0，然后解关于m的不等式即可；
（2）先把点A的坐标代入反比例函数表达式客求出m的值，接下来，再证明△BCN∽△ACM，依据相似三角形的性质可求得BN=1，然后将y=-1代入反比例函数的解析式可求得点B的横坐标，最后由点A和点B的坐标可求得直线AB的解析式；
（3）依据函数图像确定出一次函数图像位于反比例函数图像上方时，自变量的取值范围即可.