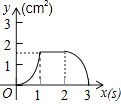
题目内容
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )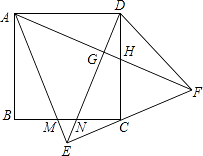
A.2个
B.3个
C.4个
D.5个
【答案】B
【解析】解:如图,连接AC、以D为圆心DA为半径画圆.
∵四边形ABCD是正方形,
∴DA=DC=AB=BC,∠ADC=∠B=∠DCB=90°,∠ACD=∠DAC=45°
∵△DEF是由△DEA翻折得到,
∴DA=DF=DC,EA=EF,∠AED=∠DEF,
∴∠AFC= ![]() ∠ADC=45°
∠ADC=45°
∴∠EFA=∠EAF=45°,
∴∠AEF=90°,
∴∠DEF=∠DEA=45°,
∵EA=ED=EF,
∴∠DAE=∠ADE=∠EDF=∠EFD=67.5°,
∴∠DAF=∠DFA=22.5°,
∴∠ADF=180°﹣∠DAF﹣∠DFA=135°,
∴∠CDF=∠ADF﹣∠ADC=45°,
∴∠DCF=180°﹣∠CDF﹣∠DFC=67.5°,
∵∠CHF=∠CDF+∠DFA=67.5°,
∴∠HCF=∠FHC,
∴△CFH是等腰三角形,故③正确.②错误,
∵∠ACD=∠CDF,
∴AC∥DF,
∴S△DFA=S△FDC,
∴S△ADH=S△CHF,故⑤正确,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠BAM=∠CDN,
在△ABM和△DCN中,
 ,
,
∴△ABM≌△DCN,故①正确,
在△EAF中,∵∠CAE=∠CAF,∠AEC=90°,作CK⊥AF于K,
∴CE=CK<CF,
∴CE≠CF故④错误.
∴①③⑤正确,
选B.

【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.