Question

【题目】已知一次函数，完成下列问题：

（1）求此函数图像与x轴、y轴的交点坐标；

（2）画出此函数的图像；观察图像，当时，x的取值范围是 ；

（3）平移一次函数的图像后经过点（-3，1），求平移后的函数表达式．

Answer 1

【答案】（1）函数与y轴的交点坐标为（0，4），与x轴的交点坐标（2，0）；

（2）画函数的图像见解析，x的取值范围是0≤x≤2；

（3）平移后的直线函数表达式为：y=-2x-5．

【解析】分析：（1）分别求出直线与x轴、y轴的交点，画出函数图象即可；

（2）根据函数图象与坐标轴的交点可直接得出结论；（3）设平移后的函数表达式为y=-2x+b，把（-3，1）代入求出b的值即可得出结论．

本题解析：（1）当x=0时y=4，

∴函数y=-2x+4的图像与y轴的交点坐标为（0，4）；

当y=0时，-2x+4=0，解得：x=2，

∴函数y=-2x+4的图像与x轴的交点坐标（2，0）．

（2）如图：

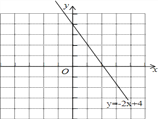
观察图像，当0≤y≤4时，x的取值范围是0≤x≤2．

（3）解：设平移后的函数表达式为y=-2x+b，将（-3，1）代入得：6+b=1，

∴b=-5,∴y=-2x-5．

∴平移后的直线函数表达式为：y=-2x-5

点睛;本题考查的是一次函数图象上点的坐标特征, 一次函数的图象, 一次函数图象与几何变换,熟知一次函数图象上各点的坐标一定适合函数的解析式是解答本题的关键.