题目内容
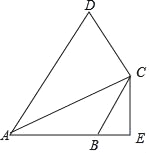
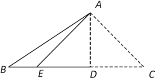
【题目】如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处．若BC=10，BE=2，则AB2－AC2的值为 ______．
【答案】20
【解析】
根据折叠的性质得到AE=AC，DE=CD，AD⊥BC，由勾股定理得到AB2=AD2+BD2，AC2=AD2+CD2，两式相减，通过整式的化简即可得到结论．
∵将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处，∴AE=AC，DE=CD，AD⊥BC，∴AB2=AD2+BD2，AC2=AD2+CD2，∴AB2﹣AC2=AD2+BD2﹣AD2﹣CD2=BD2﹣CD2=（BD+CD）（BD﹣CD）=BCBE．
∵BC=10，BE=2，∴AB2﹣AC2=10×2=20．
故答案为：20．
练习册系列答案
相关题目
