��Ŀ����
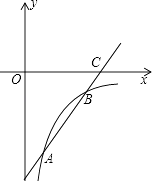
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���Ӧ��C��D������AC��BD��
��1�������C��D�����ꣻ
��2����y����һ��P��0��m����mΪ������ʹ����x��y�Ķ�Ԫһ�η�����![]() ���������⣬���P�����ꣻ
���������⣬���P�����ꣻ
��3���ڣ�2���������£���Q�����߶�CD�ϣ�������Ϊn����PBQ�����S��PBQ��ֵ��С��0.6�Ҳ�����4����n��ȡֵ��Χ��

���𰸡���1��C��0��2����D��4��2������2��P��0����4������3��2.5��n��4��
��������
��1������ƽ�ƹ��ɣ�ֱ�ӵó���C��D�����ꣻ
��2�����x��![]() .�ɵ�m��ȡֵΪ��4����P������������
.�ɵ�m��ȡֵΪ��4����P������������
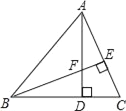
��3������P��x���ƽ���ߣ�����B��y���ƽ���߽�CD�ڵ�F����ƽ��ֱ�߽��ڵ�E�����S�ı���PEFC��3��6��18.����n��ʾ����PBQ��������ⲻ��ʽ��ɵó���.
�⣺��1���ߵ�A��B������ֱ�Ϊ����1��0������3��0��������A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ�õ���Ӧ��C��D��
��C��0��2����D��4��2����
��2�� ��
��
���+�ڵã�
x��![]() .
.
��x��������
��m����3.
��m����4ʱ�������������������![]() ��
��
��P��0����4����
��3������P��x���ƽ���ߣ�����B��y���ƽ���߽�CD�ڵ�F����ƽ��ֱ�߽��ڵ�E��

��S�ı���PEFC��3��6��18.
S�ı���PEFC��![]() +
+![]() ��3��4+
��3��4+![]() ��2��(3��n).
��2��(3��n).
��3n+S��PBQ+6+3��n��18.
��S��PBQ��9��2n.
��S��PBQ��ֵ��С��0.6�Ҳ�����4��
��0.6��9��2n��4.
���2.5��n��4.2.
�֡�Q�����߶�CD�ϣ�
��0��n��4��
��n��ȡֵ��Χ��2.5��n��4.

 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�