题目内容
【题目】已知:如图,AB是⊙O的直径,C是⊙O上的一点,且∠BCE=∠CAB,CE交AB的延长线于点E,AD⊥AB,交EC的延长线于点D.
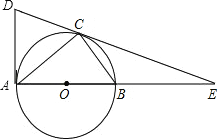
(1)判断直线DE与⊙O的位置关系,并证明你的结论;
(2)若CE=3,BE=2,求CD的长.
【答案】(1)DE是⊙O的切线;(2)CD=![]() .
.
【解析】解:(1)直线DE与⊙O相切;
证明:如图,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵OA=OC,
∴∠OAC=∠ACO.
∵∠BCE=∠CAB,
∴∠BCE=∠ACO.
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠BCE+∠BCO=∠BCO+∠ACO=∠OCE=90°.
∴DE是⊙O的切线.
(2)∵EC是圆O的切线,
∴CE2=BEAE.
∵CE=3,BE=2,
∴AE=![]() .
.
∵AD⊥AB,AB是⊙O的直径,
∴DA是⊙O的切线.
∴AD=CD.
∵AD2+AE2=DE2,
∴CD2+(![]() )2=(CD+3)2,
)2=(CD+3)2,
∴CD=![]() .
.


练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目