题目内容
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(3,a)(其中a>4),射线OA与反比例函数y=![]() 的图象交于点P,点B、C分别在函数y=
的图象交于点P,点B、C分别在函数y=![]() 的图象上,且AB∥x轴,AC∥y轴;
的图象上,且AB∥x轴,AC∥y轴;
(1)当点P横坐标为2,求直线AO的表达式;
(2)连接CO,当AC=CO时,求点A坐标;
(3)连接BP、CP,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.

【答案】(1)y=3x;(2)点A(3,9);(3)比值为1.
【解析】
(1)把x=2代入反比例解析式求出y的值,确定出P坐标,将P坐标代入直线AO解析式y=kx,求出k的值,即可确定出解析式;
(2)连接CO,如图1所示,由AC与y轴平行,得到A与C横坐标相同,确定出C坐标,求出OC的长,即为AC的长,列出方程,求出解即可确定出A坐标;
(3)![]() 的值不变,理由为:如图2,过C点向y轴作垂线交OA于点D,连接BD,作BE⊥AD,CF⊥AD,垂足分别为E、F,连接BP,CP,根据A坐标表示出直线OC解析式,进而表示出D坐标,以及B坐标,得到四边形ABCD为矩形,进而得到BE=CF,利用同底等高三角形面积相等即可求出所求之比.
的值不变,理由为:如图2,过C点向y轴作垂线交OA于点D,连接BD,作BE⊥AD,CF⊥AD,垂足分别为E、F,连接BP,CP,根据A坐标表示出直线OC解析式,进而表示出D坐标,以及B坐标,得到四边形ABCD为矩形,进而得到BE=CF,利用同底等高三角形面积相等即可求出所求之比.
(1)当x=2时,y=![]() =6,
=6,
∴P(2,6),
设直线AO的解析式为y=kx,
代入P(2,6)得k=3,
则直线AO的解析式为y=3x;
(2)如图1,连接OC,
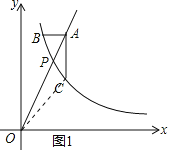
由AC∥y轴,得C点横坐标为3.
当x=3时,y=4,
∴C(3,4),即OC=![]() =5,
=5,
∵AC=OC,
∴a-4=5,即a=9,
∴A(3,9);
(3)![]() 的值不变,理由为:
的值不变,理由为:
如图2,过C点向y轴作垂线交OA于点D,连接BD,作BE⊥AD,CF⊥AD,垂足分别为E、F,连接BP,CP,

∵直线OA的解析式为y=![]() x,
x,
∴D点的坐标为(![]() ,4),
,4),
∵AB∥x轴,
∴点B的坐标为(![]() ,a).
,a).
∴CD∥x轴,
∴四边形ABCD是矩形,
∴B、C到对角线AD的距离相等,即BE=CF,
∴△ABP与△ACP是同底等高的两个三角形,它们面积相等,
则![]() =1.
=1.