题目内容
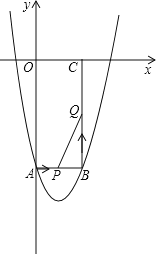
【题目】如图,在平面直角坐标系xOy中,二次函数![]() 的图象与y轴交于C点,与x轴交于A、B两点(A点在B点右侧),一次函数
的图象与y轴交于C点,与x轴交于A、B两点(A点在B点右侧),一次函数![]() 的图象经过A、C两点,已知
的图象经过A、C两点,已知![]() .
.
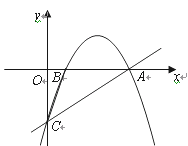
(1)求该二次函数和一次函数的解析式
(2)连接BC,求△ABC的面积
【答案】(1) ![]() ; (2)3.
; (2)3.
【解析】
(1)由二次函数y=![]() x2+bx2的解析式可求出和y轴交点的坐标即点C的坐标,由已知条件求出OA的长度进而求出点A的坐标,把A,C的坐标分别代入即可求出二次函数和一次函数的解析式;
x2+bx2的解析式可求出和y轴交点的坐标即点C的坐标,由已知条件求出OA的长度进而求出点A的坐标,把A,C的坐标分别代入即可求出二次函数和一次函数的解析式;
(2)令y=0,求出B点的坐标即OB的长度,所以AB的长度可以求出,又因为AB上的高为OC,利用面积公式即可求出△ABC的面积.
(1)在y=![]() x2+bx2中,
x2+bx2中,
令x=0,得y=-2,
∴C(0,-2),
∴OC=2,
在Rt△AOC中,OA=![]() =4,
=4,
∴A(4,0).
∵y=![]() x2+bx2过A(4,0),
x2+bx2过A(4,0),
∴0=![]() ×42+b×42,
×42+b×42,
∴b=![]() ,
,
∴y=![]() x2+
x2+![]() x2.
x2.
∵y=mx+n(m≠0)过A(4,0)、C(0,-2),
∴![]() ,
,
∴ ,
,
∴y=![]() x-2;
x-2;
(2)在y=![]() x2+
x2+![]() x2中,
x2中,
令y=0,得x1=1,x2=4,
∴B(1,0),
∴OB=1,
∴AB=OA-OB=3,
∴S△ABC=![]() ×ABOC=
×ABOC=![]() ×3×2=3.
×3×2=3.

 字词句段篇系列答案
字词句段篇系列答案【题目】为了调查甲,乙两台包装机分装标准质量为![]() 奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:![]() )如下:
)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量( | 甲 | 乙 |
| ____________ | 0 |
| 0 | 3 |
| 3 | 1 |
| 0 | ____________ |
| ____________ | 1 |
| 3 | 0 |
分析数据:
表二
种类 | 甲 | 乙 |
平均数 | 401.5 | 400.8 |
中位数 | ____________ | 402 |
众数 | 400 | ____________ |
方差 | 36.85 | 8.56 |
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.