题目内容
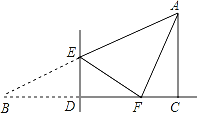
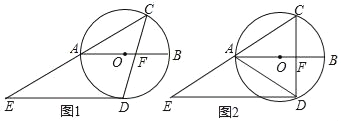
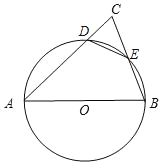
【题目】如图,AB为⊙O的直径,△ABC的边AC,BC分别与⊙O交于D,E,若E为![]() 的中点.
的中点.
(1)求证:DE=EC;
(2)若DC=2,BC=6,求⊙O的半径
【答案】(1)证明见解析;(2)4.5.
【解析】
(1)连结AE、BD,由E为![]() 的中点可得AE是∠CAB的平分线,再由直径所对的圆周角为直角可知∠AEB=∠AEC=90°,故可证
的中点可得AE是∠CAB的平分线,再由直径所对的圆周角为直角可知∠AEB=∠AEC=90°,故可证![]() ,则CE=EB=DE;
,则CE=EB=DE;
(2)设半径为r,则可得AB=AC=2r,则AD=AC-CD=2r-2,在Rt△CBD中运用勾股定理求解BD,再在Rt△ABD中运用勾股定理即可求解.
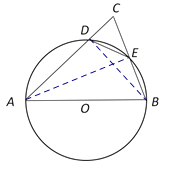
(1)连结AE,BD
∵E为![]() 的中点
的中点
∴![]() =
= ![]() ,
,
∠CAE=∠BAE-
∵∠AEB是直径所对的圆周角
∴∠AEB=90°
即AE⊥BC
∴∠AEB=∠AEC=90°
在![]() 和
和![]() 中
中
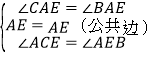 ,
,
∴![]() (ASA)
(ASA)
∴CE=BE
∴DE=CE=BE=![]() BC;
BC;
(2)在Rt△CBD中,
![]()
设半径为r,则AB=2r,
由(1)得AC=AB=2r
AD=AC-CD=2r-2
在Rt△ABD中
![]()
∴![]()
求得r=4.5.

【题目】为了调查甲,乙两台包装机分装标准质量为![]() 奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:![]() )如下:
)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量( | 甲 | 乙 |
| ____________ | 0 |
| 0 | 3 |
| 3 | 1 |
| 0 | ____________ |
| ____________ | 1 |
| 3 | 0 |
分析数据:
表二
种类 | 甲 | 乙 |
平均数 | 401.5 | 400.8 |
中位数 | ____________ | 402 |
众数 | 400 | ____________ |
方差 | 36.85 | 8.56 |
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.