题目内容
【题目】在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-![]() ,-
,-![]() ),(-
),(-![]() ,-
,-![]() ),…,都是和谐点.
),…,都是和谐点.
(1)分别判断函数y=-2x+1和y=x2+1的图象上是否存在和谐点,若存在,求出其和谐点的坐标;
(2)若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点(![]() ,
,![]() ),且当0≤x≤m时,函数y=ax2+4x+c-
),且当0≤x≤m时,函数y=ax2+4x+c-![]() (a≠0)的最小值为-3,最大值为1,求m的取值范围.
(a≠0)的最小值为-3,最大值为1,求m的取值范围.
(3)直线l:y=kx+2经过和谐点P,与x轴交于点D,与反比例函数G:y=![]() 的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且DM+DN<3
的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且DM+DN<3![]() ,请直接写出n的取值范围.
,请直接写出n的取值范围.
【答案】(1)不存在;(2)2≤m≤4;(3)-![]() <n<0或0<n<1.
<n<0或0<n<1.
【解析】
(1)根据和谐点的横坐标与纵坐标相同,可得关于a的方程,根据解方程,可得答案.
(2)根据和谐点的概念令ax2+4x+c=x,即ax2+3x+c=0,由题意,△=32-4ac=0,即4ac=9,方程的根为![]() ,从而求得a=-1,c=
,从而求得a=-1,c=![]() ,所以函数y=ax2+4x+c-
,所以函数y=ax2+4x+c-![]() =-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
=-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
(3)根据题意得出当n>0时,以及当n<0时,分别利用数形结合得出n的取值.
(1)存在,
令-2x+1=x,解得x=![]() ,
,
∴函数y=-2x+1的图象上有一个和谐点(![]() ,
,![]() );
);
令x2+1=x,即x2-x+1=0,
∵根的判别式△=(-1)2-4×1×1=-3<0,
∴方程x2-x+1=0无实数根,
∴函数y=x2+1的图象上不存在和谐点.
(2)令ax2+4x+c=x,即ax2+3x+c=0,
由题意,△=32-4ac=0,即4ac=9,
又方程的根为![]() ,
,
解得a=-1,c=![]() .
.
故函数y=ax2+4x+c![]() ,即y=-x2+4x-3,
,即y=-x2+4x-3,
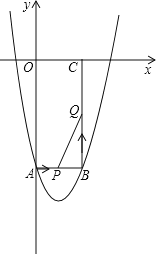
如图1,该函数图象顶点为(2,1),与y轴交点为(0,-3),由对称性,该函数图象也经过点(4,-3).

由于函数图象在对称轴x=2左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小,且当0≤x≤m时,函数y=-x2+4x-3的最小值为-3,最大值为1,
∴2≤m≤4.
(3)![]() <n<0,或0<n<1.
<n<0,或0<n<1.
∵y=kx+2经过和谐点P,
∴y=x,
∴x=kx+2,
∴点P的横坐标为1,
∴k=-1,
∴直线l为:y=-x+2,
分两种情况:
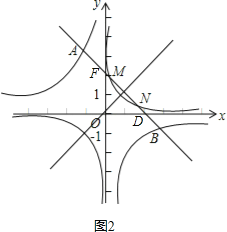
①如图2,当
∵y=-x+2,与x轴交于点D(2,0),与y轴交于点F(0,2),
∴DF=2![]() ,
,
∴DM+DN<3![]() ,
,
∴只要y=-x+2与y=![]() 有交点坐标即可,
有交点坐标即可,
∴-x+2=![]() ,
,
整理得:x2-2x+n=0,
∴b2-4ac>0,
∴4-4n>0,
解得:n<1,
则0<n<1;
②如图3,
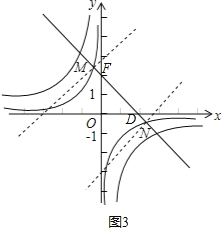
当n<0时,当DM+DN=3![]() ,
,
则DN=FM=![]() ,
,
∵y=-x+2,与x轴交于点D(2,0),与y轴交于点F(0,2),
∴可求出M(-![]() ,
,![]() ),
),
则xy=n=-![]() ,
,
则-![]() <n<0.
<n<0.
综上,当-![]() <n<0或0<n<1时,反比例函数G2的图象与直线l有两个公共点M,N,且DM+DN<3
<n<0或0<n<1时,反比例函数G2的图象与直线l有两个公共点M,N,且DM+DN<3![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了调查甲,乙两台包装机分装标准质量为![]() 奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:![]() )如下:
)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量( | 甲 | 乙 |
| ____________ | 0 |
| 0 | 3 |
| 3 | 1 |
| 0 | ____________ |
| ____________ | 1 |
| 3 | 0 |
分析数据:
表二
种类 | 甲 | 乙 |
平均数 | 401.5 | 400.8 |
中位数 | ____________ | 402 |
众数 | 400 | ____________ |
方差 | 36.85 | 8.56 |
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.