题目内容
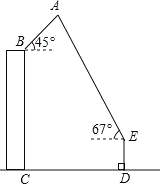
【题目】已知△ABC中,∠BAC=90°,用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形,其作法不正确的是_______.(填序号)
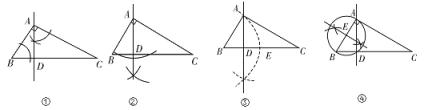
【答案】③
【解析】
根据过直线外一点作这条直线的垂线,及线段中垂线的做法,圆周角定理,分别作出直角三角形斜边上的垂线,根据直角三角形斜边上的垂线,把原直角三角形分成了两个小直角三角形,图中的三个直角三角形式彼此相似的;即可作出判断.
①、在角∠BAC内作作∠CAD=∠B,交BC于点D,根据余角的定义及等量代换得出∠B+∠BAD=90°,进而得出AD⊥BC,根据直角三角形斜边上的垂线,把原直角三角形分成了两个小直角三角形,图中的三个直角三角形式彼此相似的;
②、以点A为圆心,略小于AB的长为半径,画弧,交线段BC两点,再分别以这两点为圆心,大于![]() 两交点间的距离为半径画弧,两弧相交于一点,过这一点与A点作直线,该直线是BC的垂线;根据直角三角形斜边上的垂线,把原直角三角形分成了两个小直角三角形,图中的三个直角三角形是彼此相似的;
两交点间的距离为半径画弧,两弧相交于一点,过这一点与A点作直线,该直线是BC的垂线;根据直角三角形斜边上的垂线,把原直角三角形分成了两个小直角三角形,图中的三个直角三角形是彼此相似的;
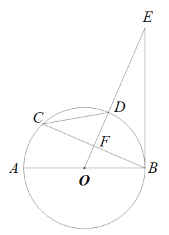
③、以点B为圆心BA的长为半径画弧,交BC于点E,再以E点为圆心,AB的长为半径画弧,在BC的另一侧交前弧于一点,过这一点及A点作直线,该直线不一定是BE的垂线;从而就不能保证两个小三角形相似;
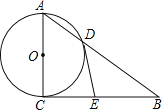
④、以AB为直径作圆,该圆交BC于点D,根据圆周角定理,过AD两点作直线该直线垂直于BC,根据直角三角形斜边上的垂线,把原直角三角形分成了两个小直角三角形,图中的三个直角三角形式彼此相似的;
故答案为:③.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目