Question

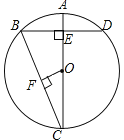
【题目】如图，AB是⊙O的直径， OE垂直于弦BC，垂足为F，OE交⊙O于点D，且∠CBE=2∠C．

（1）求证：BE与⊙O相切；

（2）若DF=9，tanC=，求直径AB的长．

Answer 1

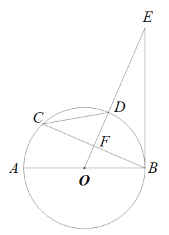
【答案】（1）见解析；（2）25

【解析】

（1）由OE垂直于弦BC，可证∠BOE+∠OBF=90°，由圆周角定理可得∠BOE=2∠C，从而∠CBE=∠BOE，进而可证BE与⊙O相切；

（2）由DF=9，tanC=，可求出CF=BF=12，设半径长是x，在Rt△BOF中，利用勾股定理列方程求解即可．

（1）证明：∵OE垂直于弦BC，

∴∠BOE+∠OBF=90°，

∵∠CBE=2∠C， ∠BOE=2∠C，

∴∠CBE=∠BOE，

∴∠CBE+∠OBF=90°，

∴∠OBE=90°，

∴BE与⊙O相切；

（2）解：∵OE垂直于弦BC，

∴∠CFD=∠BFO=90°，CF=BF．

∵DF=9，tanC=，

∴CF=BF=12．

设半径长是x，则OF=x-9，

在Rt△BOF中，

∵x2=(x-9)2+122，

∴x=，

∴直径AB=25．