题目内容
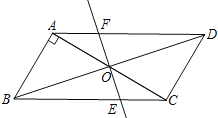
【题目】如图,在平行四边形ABCD中(BC>AB),过A作AF⊥BC,垂足为F,过C作CH⊥AB,垂足为H,交AF于G,点E为FC上一点,且GE⊥ED.
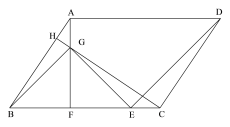
(1)若FC=2BF=4,AB=![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
(2) 若AF=FC,F为BE中点,求证:![]() .
.
【答案】(1)24;(2)见解析.
【解析】
(1)由勾股定理求出AF的长度,然后即可求出面积;
(2)连接AC,先证△ABF≌△CGF,得AG=CE,再证△AGC≌△ECD,得ED=AC,就可以证明![]() .
.
解:(1)∵FC=2BF=4,
∴BF=2,BC=2+4=6,
∵AF⊥BC,
∴∠AFB=90°,
在直角三角形ABF中,由勾股定理得,
![]() ,
,
∴平行四边形ABCD的面积为:![]() ;
;
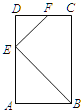
(2)连接AC,如图:
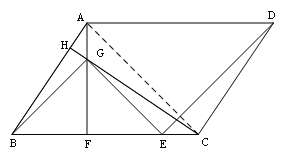 ,
,
∵AF⊥BC,CH⊥AB,
∴∠AFB=∠CFG=∠CHB=90°,
∴∠ABF+∠BAF=∠ABF+∠BCH=90°,
∴∠BAF=∠BCH,
∵AF=CF,
∴△ABF≌△CGF,
∴BF=GF,AB=CG=CD,
∵F为BE中点,
∴BF=GF=EF,
∴![]() ,
,
即AG=CE,
∵∠AGC=∠GFC+∠BCH=90°+∠BCH,
∠BAD=∠GAD+∠BAF=90°+∠BAF,
∴∠AGC=∠BAD=∠ECD,
∴△ACG≌△EDC,
∴AC=DE,
∵在直角三角形ACF中,由勾股定理,得
![]() ,
,
∵AD+AG=BC+CE=2EF+2CE=2CF,
即![]()
∴![]() ,
,
∴![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案【题目】甲、乙两位同学5次数学选拔赛的成绩统计如下表,他们5次考试的总成绩相同,请同学们完成下列问题:
第1 次 | 第2 次 | 第 3次 | 第 4次 | 第5 次 | |
甲成绩 | 90 | 40 | 70 | 40 | 60 |
乙成绩 | 70 | 50 | 70 |
| 70 |
(1)统计表中,求![]() 的值,甲同学成绩的极差为多少;
的值,甲同学成绩的极差为多少;
(2)小颖计算了甲同学的成绩平均数为60,方差是![]() [(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]=360.
[(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]=360.
请你求出乙同学成绩的平均数和方差;
(3)从平均数和方差的角度分析,甲乙两位同学谁的成绩更稳定.