题目内容
 如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=2,AB=12,BO=13.则sin∠OAC的值为________.
如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=2,AB=12,BO=13.则sin∠OAC的值为________.

分析:由AB为圆O的切线,根据切线性质得到∠OAB=90°,即三角形OAB为直角三角形,由AB与BO的长,利用勾股定理求出OA的长,然后在直角三角形AOH中,由OH和OA的长,利用锐角三角函数的定义即可求出sin∠OAC的值.
解答:∵AB是⊙O的切线,
∴∠OAB=90°,又AB=12,BO=13,
根据勾股定理得:OA=
 =5,又OH=2,
=5,又OH=2,在直角三角形OAH中,根据锐角三角函数的定义得:
sin∠OAC=
 =
= .
.故答案为:

点评:此题考查了切线的性质,勾股定理及锐角三角函数的定义.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.同时要求学生掌握正弦函数的定义:在直角三角形中,锐角A的对边与斜边的比叫做角A的正弦,记作sinA.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
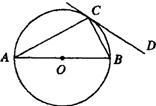 12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=
12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=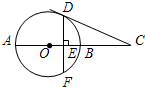 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )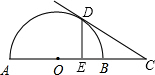
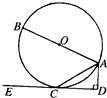 21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD.
21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD. 如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为
如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为