题目内容
12、已知，如图，AB是⊙O的直径，DC切⊙O于点C，AB=2BC，则∠BCD=30
度．分析：运用切线的性质定理以及圆周角定理计算．
解答：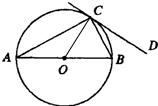
解：连接OC，
∵AB是直径，
∴∠ACB=90°，
∵AB=2BC，
∴∠A=30°，
∵OA=OC，
∴∠ACO=∠A=30°；
∴∠BCO=60°，
∵DC切⊙O于点C，
∴∠OCD=90°，
∴∠BCD=30°．
解：连接OC，∵AB是直径，
∴∠ACB=90°，
∵AB=2BC，
∴∠A=30°，
∵OA=OC，
∴∠ACO=∠A=30°；
∴∠BCO=60°，
∵DC切⊙O于点C，
∴∠OCD=90°，
∴∠BCD=30°．
点评：本题考查了运用了切线的性质定理以及圆周角定理解决实际问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
22、已知：如图，AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC．
（2013•门头沟区一模）已知：如图，AB是⊙O的直径，AC是⊙O的弦，M为AB上一点，过点M作DM⊥AB，交弦AC于点E，交⊙O于点F，且DC=DE．
（1997•昆明）已知：如图，AB是⊙O的直径，直线MN切⊙O于点C，AD⊥MN于D，AD交⊙O于E，AB的延长线交MN于点P．求证：AC2=AE•AP．
（2012•平谷区二模）已知，如图，AB是⊙O的直径，点E是
已知：如图，AB是⊙O的直径，BC为⊙O的切线，过点B的弦BD⊥OC交⊙O于点D，垂足为E．