题目内容
如图，AB是半圆的直径，O是圆心，C是AB延长线上一点，CD切半圆于D，DE⊥AB于E．已知AE：EB=4：1，CD=2，求BC的长．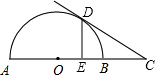
分析：先利用圆的切割线定理列出等量关系式，再根据已知条件代入相应的数，列出函数式求解．
解答：解：设EB=x，则AE=4x，设CB=y
∵CD是⊙O的切线，由圆的切割线定理得出CD2=CB•CA，
即4=y（y+5x）①（2分）
∵AB是直径，且DE⊥AB于E，
∴DE2=AE•EB=4x•x=4x2（1分）
又EC=x+y，CD=2，∠DEC=90°，
∴DE2+EC2=CD2
即4x2+（x+y）2=4④（2分）
解由①、②组成的方程组，②-①，得
5x2-3xy=0，∴x（5x-3y）=0
∴x=0（舍去）或x=
y把x=
y代入①，得
y=-1（舍去）或y=1
∴y=1
∴BC=y=1
答：BC的长为1．（3分）
∵CD是⊙O的切线，由圆的切割线定理得出CD2=CB•CA，
即4=y（y+5x）①（2分）
∵AB是直径，且DE⊥AB于E，
∴DE2=AE•EB=4x•x=4x2（1分）
又EC=x+y，CD=2，∠DEC=90°，
∴DE2+EC2=CD2
即4x2+（x+y）2=4④（2分）
解由①、②组成的方程组，②-①，得
5x2-3xy=0，∴x（5x-3y）=0
∴x=0（舍去）或x=
| 3 |
| 5 |
| 3 |
| 5 |
y=-1（舍去）或y=1
∴y=1
∴BC=y=1
答：BC的长为1．（3分）
点评：解决此类题应掌握圆的切线的性质，并能列出等量关系式，再求解，然后判断所求的解是否符合题意，舍去不合题意的解．
练习册系列答案
相关题目
道BC的长86.96米，跑道的宽为l米．（π=3.14，结果精确到0.01）
