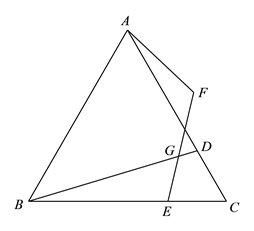
题目内容
【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]() .
.
【解析】分析: (1)连接![]() ,
,![]() ,易证
,易证![]() 是等边三角形,则
是等边三角形,则![]() 根据点
根据点![]() 与点
与点![]() 关于
关于![]() 对称,则
对称,则![]() 根据等量代换可知
根据等量代换可知![]() ;
;
(2)根据![]() ,求出
,求出![]() .因为点
.因为点![]() 与点
与点![]() 关于
关于![]() 对称,得到
对称,得到![]() ,
,![]() .则
.则![]() .
.![]() ,
,![]() ,
,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.根据圆周角定理有
为半径的圆上.根据圆周角定理有![]() .
.
(3)![]() .理由如下:连接
.理由如下:连接![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,证明
,证明![]() ,
,
得到![]() .根据
.根据![]() ,即可得到
,即可得到![]() .
.
(1)![]() ;
;
(2)如图:
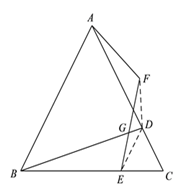
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
由(1)知![]() .
.
∴![]() ,
,![]() ,
,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
∴![]() .
.
(3)![]() .理由如下:
.理由如下:
连接![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
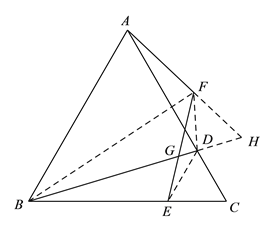
设![]() ,
,
则![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
由(2)知![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
四边形![]() 中,
中,![]() .
.
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
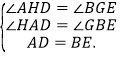
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]()
(1)画出![]() 关于坐标原点O成中心对称的
关于坐标原点O成中心对称的![]() ;
;
(2)将![]() 绕坐标原点O顺时针旋转
绕坐标原点O顺时针旋转![]() ,画出对应的
,画出对应的![]() ;
;
(3)若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,请直接写出在第一象限中的点
为顶点的四边形为平行四边形,请直接写出在第一象限中的点![]() 的坐标 .
的坐标 .
【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
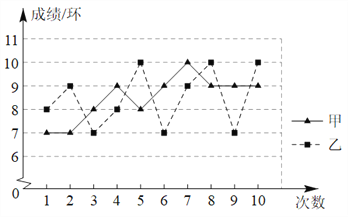
(1)根据折线图把下列表格补充完整;
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.