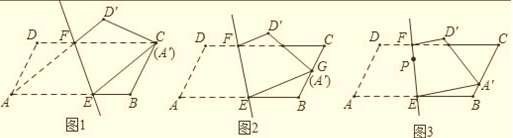
题目内容
【题目】如图,在四边形ABCD中, ∠B=90°,DE//AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.

(1)求证:△ACD是等腰三角形;
(2)若AB=4,求CD的长.
【答案】(1)详见解析;(2)8.
【解析】
试题(1)先根据条件证明△ABC≌△CED就可以得出∠CDE=∠ACB=30°,再计算出∠DCF=30°,这样就可以得出结论;
(2)根据AB=4就可以求出AC的值,就可以求出CD.
试题解析:(1)∵DE∥AB,
∴∠DEC=∠B.
在△ABC和△CED中
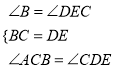 ,
,
∴△ABC≌△CED(ASA)
∴∠CDE=∠ACB=30°,
∴∠DCE=30°,
∴∠DCF=∠DCE-∠ACB=30°,
∴∠DCF=∠CDF,
∴△FCD是等腰三角形;
(2)∵∠B=90°,∠ACB=30°,
∴AC=2AB.
∵AB=4,
∴AC=8,
∴CD=8.
答:CD=8.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案【题目】某校七年级为了解课堂发言情况,随机抽取了该年级部分学生,对他们某天在课堂上发言次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图表中相关信息,回答下列问题:
,请结合图表中相关信息,回答下列问题:
组别 | 发言次数 |
|
|
|
|
|
|
|
|
|
|
|
|

(1)求出样本容量,并补全条形统计图;
(2)求![]() 组所在扇形的圆心角的度数;
组所在扇形的圆心角的度数;
(3)该年级共有学生800人,请你估计该年级在这天里发言次数不少于12的人数.
【题目】某公园的门票价格规定如表:
购票人数 | 1-50人 | 51-100人 | 100人以上 |
票价 | 10元/人 | 8元/人 | 5元/人 |
(1)某校七年组甲、乙两班共100多人去该公园举行联欢活动,其中甲班50多人,乙班不足50人,如果以班为单位分别买票,两个班一共应付920元;如果两个班联合起一作为一团体购票,一共只要付515元.问:甲、乙两班分别有多少人?
(2)若有![]() 两个团队共160人,以各自团队为单位分别买票,共用950元,问
两个团队共160人,以各自团队为单位分别买票,共用950元,问![]() 两个团队各有多少人?
两个团队各有多少人?