题目内容
【题目】如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是cm. 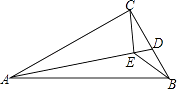
【答案】![]() ﹣6
﹣6
【解析】解:如图, 
由题意知,∠AEC=90°,
∴E在以AC为直径的⊙M的 ![]() 上(不含点C、可含点N),
上(不含点C、可含点N),
∴BE最短时,即为连接BM与⊙M的交点(图中点E′点),
∵AB=13cm,AC=12cm,BC=5cm,
∴AC2+BC2=AB2 ,
∴∠ACB=90°,
作MF⊥AB于F,
∴∠AFM=∠ACB=90°,∠FAM=∠CAB,
∴△AMF∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,得MF=
,得MF= ![]() ,
,
∴AF= ![]() =
= ![]() ,
,
则BF=AB﹣AF= ![]() ,
,
∴BM= ![]() =
= ![]() ,
,
∵ME=6,
∴BE长度的最小值BE′=BM﹣ME′= ![]() ﹣6,
﹣6,
故答案为: ![]() ﹣6.
﹣6.
由∠AEC=90°知E在以AC为直径的⊙M的 ![]() 上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.
上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: 请结合图表完成下列各题:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |

(1)表中a的值为;
(2)频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?