题目内容
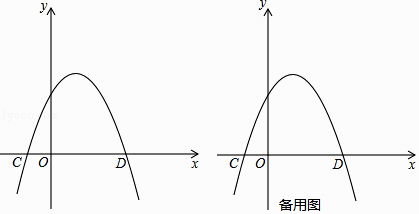
【题目】如图，点M（4，0），以点M为圆心，2为半径的圆与x轴交于点A、B，已知抛物线y= 
x2+bx+c过点A和B，与y轴交于点C．
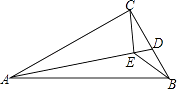
（1）求点C的坐标，并画出抛物线的大致图象．
（2）点P为此抛物线对称轴上一个动点，求PC﹣PA的最大值．
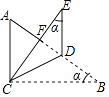
（3）CE是过点C的⊙M的切线，E是切点，CE交OA于点D，求OE所在直线的函数关系式．
【答案】
（1）
解：由题意，得
A（2，0），B（6，0）．
将A，B点坐标代入函数解析式，得
，
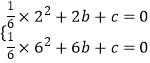解得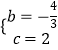 
，
函数解析式为y═ 
x2﹣ 
x+2，
当x=0时，y=2，即C点坐标为（0，2），
图象如图1
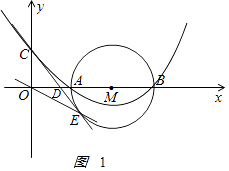
（2）
解：由三角形的两边之差小于第三边，得
PC﹣PA＜CA，
当时P，A，C在同一条直线上时，PC﹣PA=AC 
=2 
，
即PC﹣PA的最大值是2
（3）
解：如图2
，
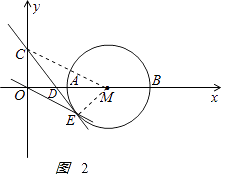连接MC，ME，
∵CE是过点C的⊙M的切线，E是切点，
∴∠MED=∠COD=90°．
在△CDO和△MED中，
，
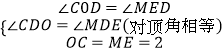∴△CDO≌△MED（AAS），
DO=DE，DC=DM，
∠DEO=∠DOE，∠MCD=∠CMD．
∵∠DEO= 
，∠MCD= 
，
∴∠MCE=∠CEO，
∴CM∥OE，
∵直线CM的解析式为y=﹣ 
x+2，
∴直线OE的解析式为y=﹣ x
【解析】（1）根据待定系数法，可得函数解析式，根据自变量与函数值得对应关系，可得C点坐标；（2）根据三角形三边的关系，可得PC﹣PA＜CA，根据线段的和差，可得答案；（3）根据全等三角形的判定与性质，可得DO=DE，DC=DM，根据等腰三角形的性质，三角形的内角和，可得∠MCE=∠CEO，根据平行线的判定与性质，可得答案．
【考点精析】本题主要考查了平行线的判定与性质和三角形三边关系的相关知识点，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边才能正确解答此题．
