题目内容
【题目】如图①,底面积为30cm2的空圆柱容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②. 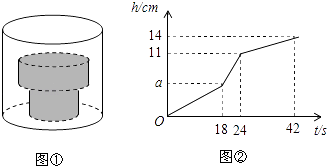
(1)求圆柱形容器的高和匀速注水的水流速度;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱体的高和底面积.
【答案】
(1)解:根据函数图象得到圆柱形容器的高为14cm,两个实心圆柱组成的“几何体”的高度为11cm,
水从刚满过由两个实心圆柱组成的“几何体”到注满用了42s﹣24s=18s,这段高度为14﹣11=3cm,
设匀速注水的水流速度为xcm3/s,则18x=303,解得x=5,
即匀速注水的水流速度为5cm3/s
(2)解:“几何体”下方圆柱的高为a,则a(30﹣15)=185,解得a=6,
所以“几何体”上方圆柱的高为11cm﹣6cm=5cm,
设“几何体”上方圆柱的底面积为Scm2,根据题意得5(30﹣S)=5(24﹣18),解得S=24,
即“几何体”上方圆柱的底面积为24cm2
【解析】(1)根据图象,分三个部分:满过“几何体”下方圆柱需18s,满过“几何体”上方圆柱需24s﹣18s=6s,注满“几何体”上面的空圆柱形容器需42s﹣24s=18s,再设匀速注水的水流速度为xcm3/s,根据圆柱的体积公式列方程,再解方程;(2)根据圆柱的体积公式得a(30﹣15)=185,解得a=6;根据圆柱的体积公式得a(30﹣15)=185,解得a=6,于是得到“几何体”上方圆柱的高为5cm,设“几何体”上方圆柱的底面积为Scm2 , 根据圆柱的体积公式得5(30﹣S)=5(24﹣18),再解方程即可.

练习册系列答案
相关题目